题目内容
16.在边长为1的正方形ABCD中,以A为起点,其余顶点为终点的向量分别为$\overrightarrow{{a}_{1}}$,$\overrightarrow{{a}_{2}}$,$\overrightarrow{{a}_{3}}$;以C为起点,其余顶点为终点的向量分别为$\overrightarrow{{c}_{1}}$,$\overrightarrow{{c}_{2}}$,$\overrightarrow{{c}_{3}}$.若m为($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)的最小值,其中{i,j}⊆{1,2,3},{s,t}⊆{1,2,3},则m=-5.分析 如图建立直角坐标系.不妨记以A为起点,其余顶点为终点的向量为$\overrightarrow{{a}_{1}}$,$\overrightarrow{{a}_{2}}$,$\overrightarrow{{a}_{3}}$分别为$\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}$,以C为起点,其余顶点为终点的向量为$\overrightarrow{{c}_{1}}$,$\overrightarrow{{c}_{2}}$,$\overrightarrow{{c}_{3}}$分别为$\overrightarrow{CD},\overrightarrow{CA},\overrightarrow{CB}$.再分类讨论当i,j,k,l取不同的值时,利用向量的坐标运算计算($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)最小值.
解答  解:不妨记以A为起点,其余顶点为终点的向量为$\overrightarrow{{a}_{1}}$,$\overrightarrow{{a}_{2}}$,$\overrightarrow{{a}_{3}}$分别为$\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}$,以C为起点,其余顶点为终点的向量为$\overrightarrow{{c}_{1}}$,$\overrightarrow{{c}_{2}}$,$\overrightarrow{{c}_{3}}$分别为$\overrightarrow{CD},\overrightarrow{CA},\overrightarrow{CB}$.如图建立坐标系.
解:不妨记以A为起点,其余顶点为终点的向量为$\overrightarrow{{a}_{1}}$,$\overrightarrow{{a}_{2}}$,$\overrightarrow{{a}_{3}}$分别为$\overrightarrow{AB},\overrightarrow{AC},\overrightarrow{AD}$,以C为起点,其余顶点为终点的向量为$\overrightarrow{{c}_{1}}$,$\overrightarrow{{c}_{2}}$,$\overrightarrow{{c}_{3}}$分别为$\overrightarrow{CD},\overrightarrow{CA},\overrightarrow{CB}$.如图建立坐标系.
(1)当i=1,j=2,s=1,t=2时,则($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)=[(1,0)+(1,1)]•[((-1,0)+(-1,-1)]=-5;
(2)当i=1,j=2,s=1,t=3时,则($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)=[(1,0)+(1,1)]•[((-1,0)+(0,-1)]=-3;
(3)当i=1,j=2,s=2,t=3时,则($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)=[(1,0)+(1,1)]•[((-1,-1)+(0,-1)]=-4;
(4)当i=1,j=3,s=1,t=2时,则($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)=[(1,0)+(0,1)]•[((-1,0)+(-1,-1)]=-3;
同样地,当i,j,s,t取其它值时,($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)=-5,-4,或-3.
则($\overrightarrow{{a}_{i}}$+$\overline{{a}_{j}}$)•($\overrightarrow{{c}_{s}}$+$\overrightarrow{{c}_{t}}$)的最小值是-5.
故答案为:-5
点评 本小题主要考查平面向量坐标表示、平面向量数量积的运算等基本知识,考查考查分类讨论、化归以及数形结合等数学思想方法,考查分析问题、解决问题的能力

 阅读快车系列答案
阅读快车系列答案
| A. | $\sqrt{13}$ | B. | $\sqrt{5}$ | C. | $\sqrt{14}$ | D. | 4 |
| A. | g(x)=cos$\frac{x}{2}$ | B. | g(x)=-sin2x | C. | g(x)=sin(2x-$\frac{π}{3}$) | D. | g(x)=sin($\frac{x}{2}$+$\frac{π}{6}$) |
| A. | $\frac{\sqrt{2}}{2}$ | B. | -$\sqrt{2}$ | C. | $\sqrt{2}$ | D. | 2 |
| A. | $\frac{7}{12}$ | B. | $\frac{2}{3}$ | C. | $\frac{3}{4}$ | D. | $\frac{1}{2}$ |
| A. | $\frac{1}{3}$ | B. | $\frac{1}{2}$ | C. | 1 | D. | $\frac{2}{3}$ |
| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
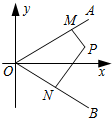 如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;
如图,射线OA,OB所在的直线的方向向量分别为$\overrightarrow{d_1}=({1,k})$,$\overrightarrow{d_2}=({1,-k})({k>0})$,点P在∠AOB内,PM⊥OA于M,PN⊥OB于N;