题目内容
18．已知点N（x，y）的坐标满足$\left\{\begin{array}{l}{2x-3y+1≤0}\\{3x+y-4≤0}\\{x≥0}\end{array}\right.$，设O为坐标原点，M（3，1），则使得$\overrightarrow{OM}$•$\overrightarrow{ON}$取得最大值时的点N的个数是（ ）| A． | 1 | B． | 2 | C． | 3 | D． | 无数 |
分析 作出可行域，由数量积可得z=$\overrightarrow{OM}$•$\overrightarrow{ON}$=3x+y，变形目标函数，平移直线可得答案．
解答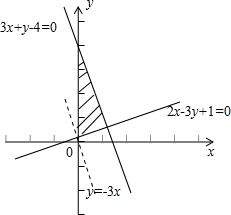 
解：作出$\left\{\begin{array}{l}{2x-3y+1≤0}\\{3x+y-4≤0}\\{x≥0}\end{array}\right.$所对应的可行域（如图阴影），
设z=$\overrightarrow{OM}$•$\overrightarrow{ON}$=3x+y，则y=-3x+z，
平移直线-3x可知，当直线与图中直线3x+y-4=0重合时，目标函数取最大值，
∴使得$\overrightarrow{OM}$•$\overrightarrow{ON}$取得最大值时的点N的个数是无数个
故选：D
点评 本题考查简单线性规划，涉及向量的数量积，准确作图是解决问题的关键，属中档题．
练习册系列答案
A加金题 系列答案
全优测试卷系列答案
相关题目
8．已知cosα=-$\frac{3}{5}$，且α∈（-π，0），则tanα=（ ）
| A． | -$\frac{4}{3}$ | B． | $\frac{4}{3}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
9．关于数列3，9，…，2187，…，以下结论正确的是（ ）
| A． | 此数列不是等差数列，也不是等比数列 | |
| B． | 此数列可能是等差数列，也可能是等比数列 | |
| C． | 此数列可能是等差数列，但不是等比数列 | |
| D． | 此数列不是等差数列，但可能是等比数列 |
13．向边长为2的正方形中随机撒一粒豆子，则豆子落在正方形的内切圆的概率是（ ）
| A． | $\frac{1}{2}$ | B． | $\frac{π}{2}$ | C． | $\frac{4}{π}$ | D． | $\frac{π}{4}$ |
3．化简$\sqrt{1+sin4}+\sqrt{1-sin4}$，得到（ ）
| A． | -2sin2 | B． | -2cos2 | C． | 2sin2 | D． | 2cos2 |
10．袋中有三个白球，两个黑球，现从袋中一次摸出两个球，在两个球颜色相同的条件下，两个球均为白球的概率是（ ）
| A． | $\frac{1}{4}$ | B． | $\frac{3}{4}$ | C． | $\frac{3}{10}$ | D． | $\frac{2}{5}$ |
7．设有一个回归方程为$\widehat{y}$=4-6x，则变量x增加一个单位时（ ）
| A． | y平均增加4个单位 | B． | y平均减少4个单位 | ||
| C． | y平均增加6个单位 | D． | y平均减少6个单位 |
8．
通过市场调查，得到某产品的资金投入x（万元）与获得的利润y（万元）的数据，如表所示：
（1）画出表中数据对应的散点图；
（2）根据上表提供的数据，用最小二乘法求线性回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）现投入资金15（万元），估计获得的利润为多少万元？
参考公式：
用最小二乘法求线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$=$\stackrel{∧}{b}$$\overline{x}$．
通过市场调查，得到某产品的资金投入x（万元）与获得的利润y（万元）的数据，如表所示：| 资金投入 x | 2 | 3 | 4 | 5 | 6 |
| 利润y | 2 | 3 | 5 | 7 | 8 |
（2）根据上表提供的数据，用最小二乘法求线性回归直线方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$；
（3）现投入资金15（万元），估计获得的利润为多少万元？
参考公式：
用最小二乘法求线性回归方程系数公式：$\stackrel{∧}{b}$=$\frac{\sum_{i-1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i-1}^{n}{x}_{i}^{2}-n{\overline{x}}^{2}}$，$\stackrel{∧}{a}$=$\overline{y}$=$\stackrel{∧}{b}$$\overline{x}$．