题目内容
8．已知cosα=-$\frac{3}{5}$，且α∈（-π，0），则tanα=（ ）| A． | -$\frac{4}{3}$ | B． | $\frac{4}{3}$ | C． | -$\frac{3}{4}$ | D． | $\frac{3}{4}$ |
分析 由cosα的值及α的范围，利用同角三角函数间的基本关系求出sinα的值，即可确定出tanα的值．
解答 解：∵cosα=-$\frac{3}{5}$＜0，且α∈（-π，0），
α的终边在第三象限
∴sinα=-$\sqrt{1-co{s}^{2}α}$=-$\frac{4}{5}$，
则tanα=$\frac{4}{3}$，
故选：B．
点评 此题考查了同角三角函数基本关系的运用，熟练掌握基本关系是解本题的关键．
练习册系列答案
培优口算题卡系列答案
开心口算题卡系列答案
口算题卡河北少年儿童出版社系列答案
相关题目
如图，从宾馆A到火车站B有A-C-B、A-D-B两条路线．出租车司机准备开车从宾馆送某旅客到火车站，若各路段发生堵车与否是相互独立的，且各路段发生堵车事件的概率如图所示（例如A-C-B算作两个路段；路段AC发生堵车事件的概率为$\frac{1}{10}$，路段CB发生堵车事件的概率为$\frac{1}{8}$）．
3．
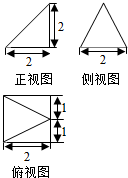已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（ ）cm2．
已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（ ）cm2．| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 2 | D． | 4 |
13．在菱形ABCD中，|$\overrightarrow{AB}$|=2，∠BAD=$\frac{π}{3}$，E为CD的中点，则$\overrightarrow{AC}$•$\overrightarrow{BE}$=（ ）
| A． | -3 | B． | 3 | C． | $\sqrt{3}$ | D． | 0 |
20．已知命题p：全等三角形面积相等；命题q：矩形对角线互相垂直．下面四个结论中正确的是（ ）
| A． | p∧q是真命题 | B． | p∨q是真命题 | C． | ￢p是真命题 | D． | ￢q是假命题 |