题目内容
13．向边长为2的正方形中随机撒一粒豆子，则豆子落在正方形的内切圆的概率是（ ）| A． | $\frac{1}{2}$ | B． | $\frac{π}{2}$ | C． | $\frac{4}{π}$ | D． | $\frac{π}{4}$ |
分析 由题意，本题是几何概型的考查，只要利用面积比可求概率．
解答 解：由题意，正方形的面积为4，其内切圆的面积为π，由几何概型的概率公式得到豆子落在正方形的内切圆的概率是：$\frac{π}{4}$；
故选D．
点评 本题考查了几何概型概率的求法；解答本题的关键是明确概率模型，利用面积比求概率．
练习册系列答案
阅读快车系列答案
相关题目
3．
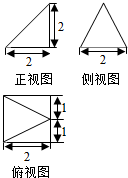已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（ ）cm2．
已知某几何体的三视图如图所示，根据图中标出的尺寸（单位：cm），可得这个几何体得体积是（ ）cm2．| A． | $\frac{4}{3}$ | B． | $\frac{8}{3}$ | C． | 2 | D． | 4 |
4．直线3x-$\sqrt{3}y$+1=0的倾斜角为（ ）
| A． | 120° | B． | 90° | C． | 60° | D． | 30° |
8．对于函数y=f（x），当x∈（0，+∞）时，总有f（x）＜xf′（x），若m＞n＞0，下列不等式中能恒成立的是（ ）
| A． | $\frac{f（m）}{m}＜\frac{f（n）}{n}$ | B． | $\frac{f（m）}{m}＞\frac{f（n）}{n}$ | C． | $\frac{f（m）}{n}＞\frac{3f（n）}{m}$ | D． | $\frac{f（m）}{n}＜\frac{f（n）}{m}$ |
2．从装有5个红球和5个黑球的口袋中任取3个球，则至少有一个红球的概率是（ ）
| A． | $\frac{1}{5}$ | B． | $\frac{1}{3}$ | C． | $\frac{1}{2}$ | D． | $\frac{11}{12}$ |