已知△ABC的顶点.A.顶点C在椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$上.则$\frac{sinA+sinB}{sinC}$=2．题目和参考答案——青夏教育精英家教网——

题目内容

14．已知△ABC的顶点，A（-2，0）和B（2，0），顶点C在椭圆$\frac{x^2}{16}+\frac{y^2}{12}=1$上，则$\frac{sinA+sinB}{sinC}$=2．

分析利用椭圆的定义及正弦定理，即可得出结论．

解答解：由题意，|CA|+|CB|=8，|AB|=4，
∴$\frac{sinA+sinB}{sinC}$=$\frac{|CA|+|CB|}{|AB|}$=2，
故答案为：2．

点评本题考查椭圆的定义及正弦定理，考查学生的计算能力，比较基础．

练习册系列答案

精英教程100分攻略系列答案

轻轻松松系列答案

心算口算巧算系列答案

三维数字课堂系列答案

实验报告系列答案

探究活动报告册系列答案

家庭作业系列答案

课堂作业同步练习系列答案

教材完全解读系列答案

课程达标测试卷系列答案

相关题目

6．已知tan（π+α）=-$\frac{1}{2}$，求下列各式的值：
（1）$\frac{2cos（π-α）-3sin（π+α）}{4cos（α-2π）+sin（4π-α）}$；
（2）sin（α-7π）cos（α+5π）．

5．已知圆M：x²+y²+2mx-3=0（m＜0）的半径为2，则椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{3}$=1（a＞0）的左焦点为F（-x，0），若垂直于x轴且经过F点的直线l与圆M相切，则a的值为（　　）

2或2$\sqrt{3}$

2．已知F₁，F₂是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的两个焦点，过点F₂的直线交椭圆于A、B两点，若|AB|=5，则|AF₁|+|BF₁|（　　）

9．M、N分别是椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）的左、右顶点，椭圆上异于M、N于点P满足k_PM•k_PN=-$\frac{1}{4}$，则椭圆的离心率为（　　）

$\frac{{\sqrt{2}}}{2}$

$\frac{{\sqrt{3}}}{3}$

$\frac{{\sqrt{3}}}{2}$

19．在平面直角坐标系xOy中，圆C与y轴相切于点M（0，2），且圆心C在直线l：y=2x-4上．
（Ⅰ）求圆C的方程；
（Ⅱ）已知过点N（4，5）的直线m与圆C交于A，B两点，且|AB|=4$\sqrt{2}$，求直线m的方程．

6．已知椭圆C：$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1（a＞b＞0）过点A（1，$\frac{\sqrt{2}}{2}$），且离心率为$\frac{\sqrt{2}}{2}$．
（1）求椭圆的标准方程；
（2）过右焦点的直线l与椭圆C相交于P，Q两点，F₁为左焦点，且$\overrightarrow{{F}_{1}P}$⊥$\overrightarrow{{F}_{1}Q}$，求直线l的方程．

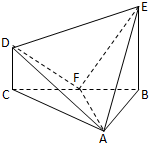在棱锥A-BCDE中，∠BAC=$\frac{π}{2}$，DC⊥平面ABC，EB⊥平面ABC，F是BC的中点，AB=AC=BE=2，CD=1．
（1）求证：EF⊥AD；
（2）求三棱锥F-ADE的高．

4．椭圆x²+$\frac{y^2}{4}$=1的离心率为（　　）

$\frac{{\sqrt{5}}}{2}$

$\frac{{\sqrt{3}}}{2}$