题目内容
2．已知F1，F2是椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1的两个焦点，过点F2的直线交椭圆于A、B两点，若|AB|=5，则|AF1|+|BF1|（ ）| A． | 11 | B． | 10 | C． | 9 | D． | 16 |
分析 由椭圆的方程求得椭圆的长轴长，再由椭圆定义结合|AB|=5求得|AF1|+|BF1|的值．
解答 解：如图，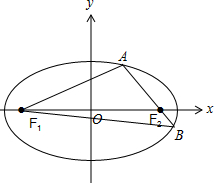
由椭圆$\frac{{x}^{2}}{16}$+$\frac{{y}^{2}}{9}$=1，得a2=16，则a=4，
又|AF1|+|BF1|+|AB|=4a=16，
且|AB|=5，∴|AF1|+|BF1|=11．
故选：A．
点评 本题考查了椭圆的标准方程，考查了椭圆的定义，是基础题．
练习册系列答案
相关题目
已知三棱锥P-ABC，底面ABC是边长为2$\sqrt{3}$的正三角形，平面PBC⊥平面ABC，PB=PC=2，D为AP上一点，AD=2DP，O是底面三角形的重心．
17．从椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1（a＞b＞0）上一点P向x轴作垂线，垂足恰为右焦点F2，A是椭圆与x轴负半轴的交点，B是椭圆与y轴正半轴的交点，且AB∥OP（O是坐标原点），则该椭圆的离心率是（ ）
| A． | $\frac{{\sqrt{2}}}{4}$ | B． | $\frac{1}{2}$ | C． | $\frac{{\sqrt{3}}}{2}$ | D． | $\frac{{\sqrt{2}}}{2}$ |
11．设椭圆的两个焦点分别为F1，F2，过F2作椭圆长轴的垂线与椭圆相交，其中的一个交点为P，若△F1PF2为等腰直角三角形，则椭圆的离心率是（ ）
| A． | $\sqrt{3}$-1 | B． | $\sqrt{2}$-1 | C． | $\frac{\sqrt{3}}{3}$ | D． | $\frac{\sqrt{2}}{2}$ |