题目内容
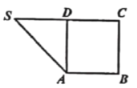
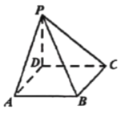
【题目】如图,在三棱柱![]() 中,
中,![]() ,
,![]() 分别是
分别是![]() ,
,![]() 的中点.
的中点.
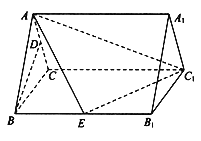
(Ⅰ)证明:![]() 平面
平面![]() ;
;
(Ⅱ)若这个三棱柱的底面是边长为2的等边三角形,側面都是正方形,求五面体![]() 的体积.
的体积.
【答案】(Ⅰ)见解析(Ⅱ)![]()
【解析】
(Ⅰ)由条件证明![]() 为平行四边形,故得
为平行四边形,故得![]() ,然后再由线面平行的判定定理可得结论成立.(Ⅱ)方法一:取
,然后再由线面平行的判定定理可得结论成立.(Ⅱ)方法一:取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,然后证明
,然后证明![]() 为四棱锥
为四棱锥![]() 的高,于是可得所求体积.方法二:取
的高,于是可得所求体积.方法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,根据条件可证得
,根据条件可证得![]() 是四棱锥
是四棱锥![]() 的高,且
的高,且![]() ,然后根据
,然后根据![]() 求解.
求解.
(Ⅰ)证明:设![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,![]() .
.
∵![]() ,
,![]() 分别为
分别为![]() ,
,![]() 的中点,
的中点,
∴![]() 且
且![]() .
.
∵![]() 为
为![]() 的中点,
的中点,
∴![]() 且
且![]() .
.
∴![]() 且
且![]() ,
,
∴![]() 为平行四边形,
为平行四边形,
∴![]() .
.
∵![]() 平面
平面![]() ,
,![]() 平面
平面![]() ,
,
∴![]() 平面
平面![]() .
.
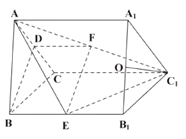
(Ⅱ)解法一:取![]() 的中点为
的中点为![]() ,连接
,连接![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵侧面是正方形,
∴![]() ,
,![]() .
.
又![]() 平面
平面![]() ,且
,且![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
又![]() ,
,
∴![]() 平面
平面![]() ,即
,即![]() 为四棱锥
为四棱锥![]() 的高.
的高.
故所求体积![]()
![]() .
.
(Ⅱ)解法二:取![]() 的中点
的中点![]() ,连接
,连接![]() ,
,
∵![]() 为等边三角形,
为等边三角形,
∴![]() .
.
∵侧面都是正方形,
∴![]() ,
,![]() .
.
∵![]() 平面
平面![]() 且
且![]() ,
,
∴![]() 平面
平面![]() .
.
∵![]() 平面
平面![]() ,
,
∴![]() ,
,
∵![]() ,
,
∴![]() 平面
平面![]() .
.
∴![]() 是四棱锥
是四棱锥![]() 的高,且
的高,且![]() .
.
故所求体积![]()
![]() .
.

练习册系列答案
 开心蛙状元作业系列答案
开心蛙状元作业系列答案 课时掌控随堂练习系列答案
课时掌控随堂练习系列答案 一课一练一本通系列答案
一课一练一本通系列答案 浙江之星学业水平测试系列答案
浙江之星学业水平测试系列答案
相关题目