题目内容
【题目】如图,在平面直角坐标系![]() 中,己知点
中,己知点![]() ,
,![]() ,
,![]() ,
,![]() 分别为线段
分别为线段![]() ,
,![]() 上的动点,满足
上的动点,满足![]() .
.
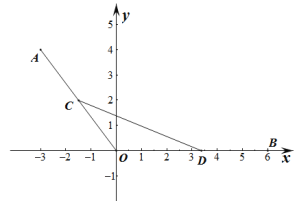
(1)若![]() 点恰好与
点恰好与![]() 点重合,求半径为
点重合,求半径为![]() 且与直线
且与直线![]() 相切于
相切于![]() 点的圆的方程;
点的圆的方程;
(2)设![]() ,求证:
,求证:![]() 的外接圆恒过定点(异于原点).
的外接圆恒过定点(异于原点).
【答案】(1)![]() 或
或![]() (2)定点为
(2)定点为![]() 证明见解析
证明见解析
【解析】
(1)当![]() 点恰好与
点恰好与![]() 点重合时,可知
点重合时,可知![]() ,
,![]() ,设出圆的圆心
,设出圆的圆心![]() 坐标为
坐标为![]() ,
,
根据![]() ,求出
,求出![]() ,即可得到圆的方程;
,即可得到圆的方程;
(2)根据![]() 三个顶点坐标,利用几何法可以求出圆的方程,即可知圆过定点.
三个顶点坐标,利用几何法可以求出圆的方程,即可知圆过定点.
(1)依题意可知,![]() ,
,![]() ,所以
,所以![]() .设圆的圆心
.设圆的圆心![]() 坐标为
坐标为![]() ,
,
由![]() ,可得,
,可得,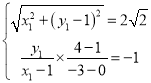 ,解得
,解得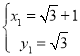 或
或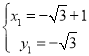 .
.
故所求的圆的方程为:![]() 或
或![]() .
.
(2)因为![]() ,设
,设![]() ,则
,则![]() ,即
,即![]() .
.
所以点![]() 的坐标为
的坐标为![]() ,点
,点![]() 的坐标为
的坐标为![]() .
.
![]() 的垂直平分线所在直线方程为:
的垂直平分线所在直线方程为:![]() ,即
,即![]() ;
;
![]() 的垂直平分线所在直线方程为:
的垂直平分线所在直线方程为:![]() ,
,
由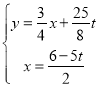 解得
解得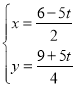 .
.
所以![]() 的外接圆的方程为:
的外接圆的方程为:![]()
即![]() ,化简得,
,化简得,![]() ,
,
令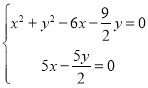 ,解得
,解得![]() (舍去)或
(舍去)或![]() .
.
故![]() 的外接圆恒过定点
的外接圆恒过定点![]() .
.

 阅读快车系列答案
阅读快车系列答案【题目】为研究女高中生身高与体重之间的关系,一调查机构从某中学中随机选取8名女高中生,其身高![]() 和体重
和体重![]() 数据如下表所示:
数据如下表所示:
编号 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
身高 | 164 | 160 | 158 | 172 | 162 | 164 | 174 | 166 |
体重 | 60 | 46 | 43 | 48 | 48 | 50 | 61 | 52 |
该调查机构绘制出该组数据的散点图后分析发现,女高中生的身高与体重之间有较强的线性相关关系.

(1)调查员甲计算得出该组数据的线性回归方程为![]() ,请你据此预报一名身高为
,请你据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(2)调查员乙仔细观察散点图发现,这8名同学中,编号为1和4的两名同学对应的点与其他同学对应的点偏差太大,于是提出这样的数据应剔除,请你按照这名调查人员的想法重新计算线性回归话中,并据此预报一名身高为![]() 的女高中生的体重;
的女高中生的体重;
(3)请你分析一下,甲和乙谁的模型得到的预测值更可靠?说明理由.
附:对于一组数据![]() ,其回归方程
,其回归方程![]() 的斜率和截距的最小二乘法估计分别为:
的斜率和截距的最小二乘法估计分别为: .
.
【题目】某小学为了解四年级学生的家庭作业用时情况,从本校四年级随机抽取了一批学生进行调查,并绘制了学生作业用时的频率分布直方图,如图所示.
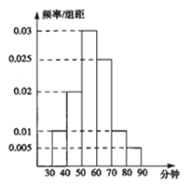
(1)估算这批学生的作业平均用时情况;
(2)作业用时不能完全反映学生学业负担情况,这与学生自身的学习习惯有很大关系如果用时四十分钟之内评价为优异,一个小时以上为一般,其它评价为良好.现从优异和良好的学生里面用分层抽样的方法抽取300人,其中女生有90人(优异20人).请完成列联表,并根据列联表分析能否在犯错误的概率不超过0.05的前提下认为学习习惯与性别有关系?
男生 | 女生 | 合计 | |
良好 | |||
优异 | |||
合计 |
附:![]() ,其中
,其中![]()
| 0.100 | 0.050 | 0.025 | 0.010 | 0.001 |
| 2.706 | 3.841 | 5.024 | 6.635 | 10.828 |