题目内容
已知二次函数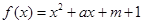 ,关于x的不等式
,关于x的不等式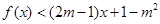 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设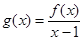 .
.
(1)求a的值;
(2)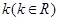 如何取值时,函数
如何取值时,函数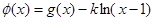 存在极值点,并求出极值点;
存在极值点,并求出极值点;
(3)若m=1,且x>0,求证: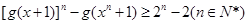
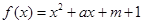 ,关于x的不等式
,关于x的不等式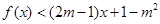 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设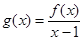 .
.(1)求a的值;
(2)
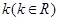 如何取值时,函数
如何取值时,函数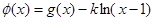 存在极值点,并求出极值点;
存在极值点,并求出极值点;(3)若m=1,且x>0,求证:
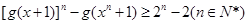
(1)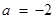 (2)当
(2)当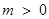 时,
时,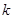 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点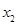 ;
;
当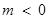 时,
时,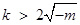 ,函数
,函数 有极小值点
有极小值点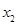 ,有极大值点
,有极大值点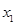 .…9分
.…9分
(其中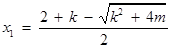 ,
, 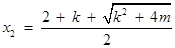 )(3)见解析
)(3)见解析
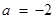 (2)当
(2)当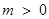 时,
时,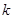 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点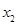 ;
;当
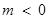 时,
时,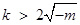 ,函数
,函数 有极小值点
有极小值点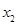 ,有极大值点
,有极大值点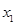 .…9分
.…9分(其中
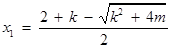 ,
, 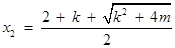 )(3)见解析
)(3)见解析(1)解:∵关于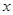 的不等式
的不等式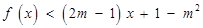 的解集为
的解集为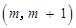 ,
,
即不等式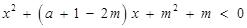 的解集为
的解集为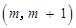 ,
,
∴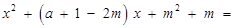
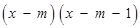 .
.
∴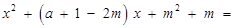
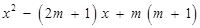 .
.
∴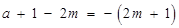 .
.
∴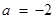 .
.
(2)解法1:由(1)得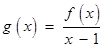
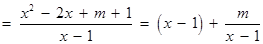 .
.
∴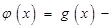
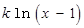
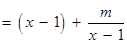
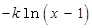 的定义域为
的定义域为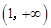 .
.
∴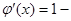
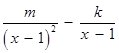
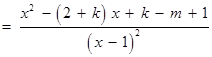 . ………3分
. ………3分
方程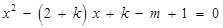 (*)的判别式
(*)的判别式
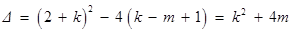 .………4分
.………4分
①当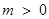 时,
时,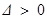 ,方程(*)的两个实根为
,方程(*)的两个实根为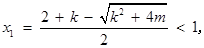
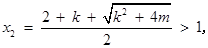 ………5分
………5分
则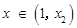 时,
时,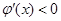 ;
;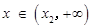 时,
时,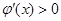 .
.
∴函数 在
在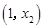 上单调递减,在
上单调递减,在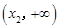 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点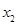 . ………6分
. ………6分
②当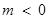 时,由
时,由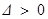 ,得
,得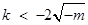 或
或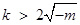 ,
,
若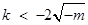 ,则
,则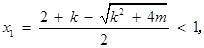
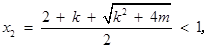
故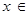
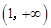 时,
时,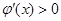 ,
,
∴函数 在
在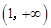 上单调递增.
上单调递增.
∴函数 没有极值点.………7分
没有极值点.………7分
若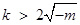 时,
时,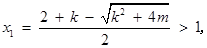
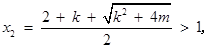
则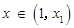 时,
时,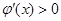 ;
;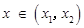 时,
时,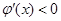 ;
;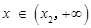 时,
时,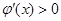 .
.
∴函数 在
在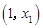 上单调递增,在
上单调递增,在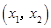 上单调递减,在
上单调递减,在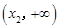 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点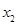 ,有极大值点
,有极大值点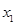 . ………8分
. ………8分
综上所述, 当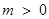 时,
时,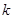 取任意实数, 函数
取任意实数, 函数 有极小值点
有极小值点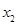 ;
;
当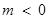 时,
时,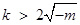 ,函数
,函数 有极小值点
有极小值点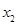 ,有极大值点
,有极大值点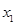 .…9分
.…9分
(其中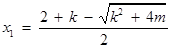 ,
, 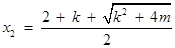 )
)
解法2:由(1)得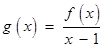
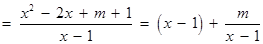 .
.
∴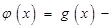
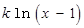
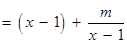
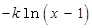 的定义域为
的定义域为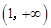 .
.
∴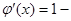
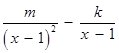
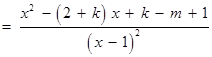 . ………3分
. ………3分
若函数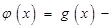
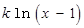 存在极值点等价于函数
存在极值点等价于函数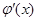 有两个不等的零点,且
有两个不等的零点,且
至少有一个零点在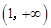 上. ………4分
上. ………4分
令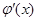
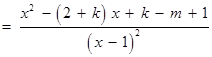
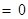 ,
,
得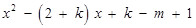
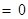 , (*)
, (*)
则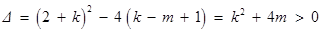 ,(**)…………5分
,(**)…………5分
方程(*)的两个实根为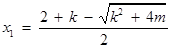 ,
, 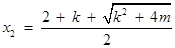 .
.
设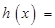
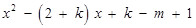 ,
,
①若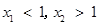 ,则
,则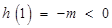 ,得
,得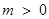 ,此时,
,此时,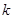 取任意实数, (**)成立.
取任意实数, (**)成立.
则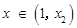 时,
时,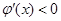 ;
;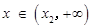 时,
时,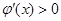 .
.
∴函数 在
在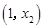 上单调递减,在
上单调递减,在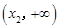 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点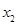 . ………6分
. ………6分
②若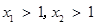 ,则
,则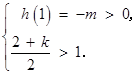 得
得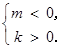
又由(**)解得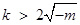 或
或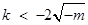 ,
,
故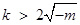 .………7分
.………7分
则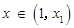 时,
时,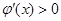 ;
;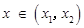 时,
时,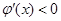 ;
;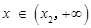 时,
时,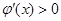 .
.
∴函数 在
在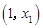 上单调递增,在
上单调递增,在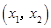 上单调递减,在
上单调递减,在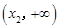 上单调递增.
上单调递增.
∴函数 有极小值点
有极小值点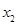 ,有极大值点
,有极大值点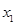 . ………8分
. ………8分
综上所述, 当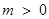 时,
时,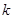 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点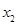 ;
;
当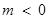 时,
时,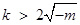 ,函数
,函数 有极小值点
有极小值点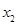 ,有极大值点
,有极大值点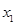 .…9分
.…9分
(其中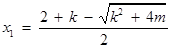 ,
, 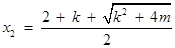 )
)
(3)∵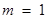 , ∴
, ∴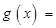
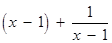 .
.
∴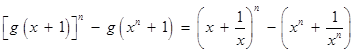
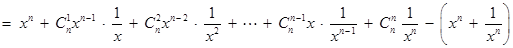
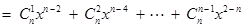 . ………10分
. ………10分
令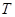
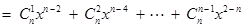 ,
,
则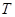
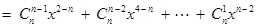
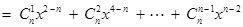 .
.
∵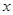
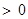 ,
,
∴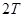
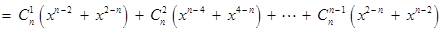 …11分
…11分
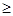
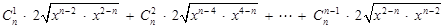 12分
12分
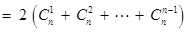
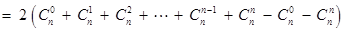
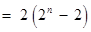 .………13分
.………13分
∴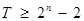 ,即
,即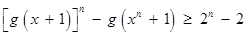 . ……………14分
. ……………14分
证法2:下面用数学归纳法证明不等式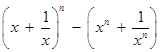
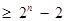 .
.
① 当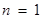 时,左边
时,左边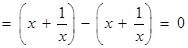 ,右边
,右边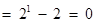 ,不等式成立;
,不等式成立;
………10分
②假设当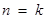
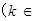 N
N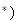 时,不等式成立,即
时,不等式成立,即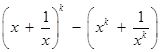
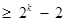 ,
,
则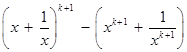
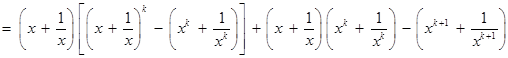
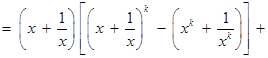
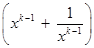 ………11分
………11分
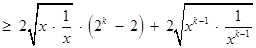 ………12分
………12分
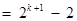 . ………13分
. ………13分
也就是说,当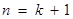 时,不等式也成立.
时,不等式也成立.
由①②可得,对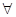
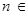 N
N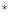 ,
,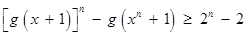 都成立. …14分
都成立. …14分
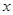 的不等式
的不等式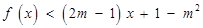 的解集为
的解集为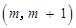 ,
,即不等式
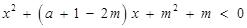 的解集为
的解集为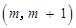 ,
,∴
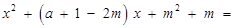
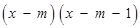 .
.∴
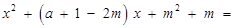
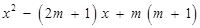 .
.∴
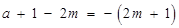 .
.∴
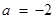 .
.(2)解法1:由(1)得
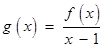
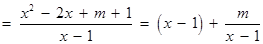 .
.∴
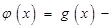
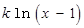
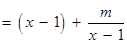
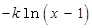 的定义域为
的定义域为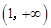 .
.∴
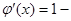
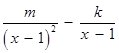
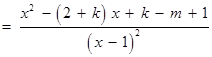 . ………3分
. ………3分方程
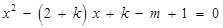 (*)的判别式
(*)的判别式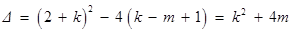 .………4分
.………4分①当
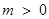 时,
时,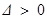 ,方程(*)的两个实根为
,方程(*)的两个实根为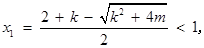
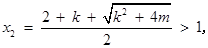 ………5分
………5分则
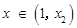 时,
时,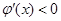 ;
;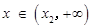 时,
时,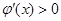 .
.∴函数
 在
在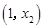 上单调递减,在
上单调递减,在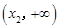 上单调递增.
上单调递增.∴函数
 有极小值点
有极小值点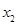 . ………6分
. ………6分②当
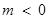 时,由
时,由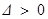 ,得
,得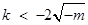 或
或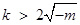 ,
, 若
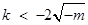 ,则
,则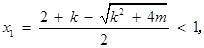
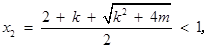
故
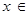
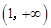 时,
时,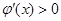 ,
, ∴函数
 在
在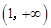 上单调递增.
上单调递增.∴函数
 没有极值点.………7分
没有极值点.………7分若
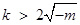 时,
时,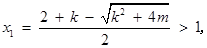
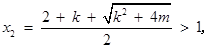
则
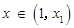 时,
时,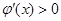 ;
;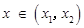 时,
时,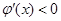 ;
;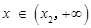 时,
时,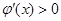 .
.∴函数
 在
在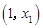 上单调递增,在
上单调递增,在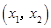 上单调递减,在
上单调递减,在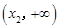 上单调递增.
上单调递增.∴函数
 有极小值点
有极小值点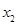 ,有极大值点
,有极大值点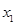 . ………8分
. ………8分综上所述, 当
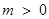 时,
时,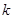 取任意实数, 函数
取任意实数, 函数 有极小值点
有极小值点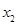 ;
;当
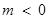 时,
时,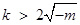 ,函数
,函数 有极小值点
有极小值点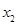 ,有极大值点
,有极大值点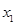 .…9分
.…9分(其中
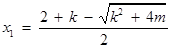 ,
, 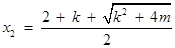 )
)解法2:由(1)得
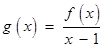
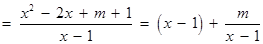 .
.∴
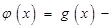
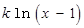
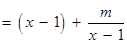
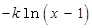 的定义域为
的定义域为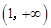 .
.∴
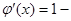
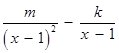
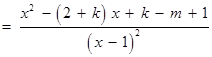 . ………3分
. ………3分若函数
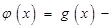
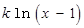 存在极值点等价于函数
存在极值点等价于函数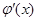 有两个不等的零点,且
有两个不等的零点,且至少有一个零点在
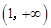 上. ………4分
上. ………4分令
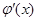
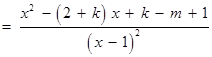
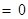 ,
,得
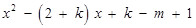
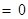 , (*)
, (*)则
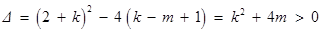 ,(**)…………5分
,(**)…………5分方程(*)的两个实根为
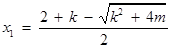 ,
, 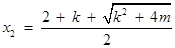 .
.设
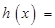
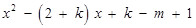 ,
,①若
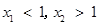 ,则
,则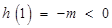 ,得
,得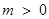 ,此时,
,此时,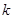 取任意实数, (**)成立.
取任意实数, (**)成立. 则
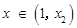 时,
时,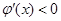 ;
;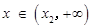 时,
时,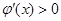 .
.∴函数
 在
在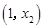 上单调递减,在
上单调递减,在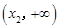 上单调递增.
上单调递增.∴函数
 有极小值点
有极小值点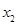 . ………6分
. ………6分②若
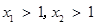 ,则
,则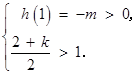 得
得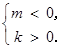
又由(**)解得
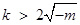 或
或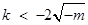 ,
,故
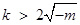 .………7分
.………7分则
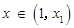 时,
时,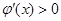 ;
;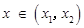 时,
时,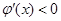 ;
;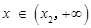 时,
时,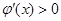 .
.∴函数
 在
在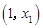 上单调递增,在
上单调递增,在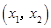 上单调递减,在
上单调递减,在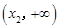 上单调递增.
上单调递增.∴函数
 有极小值点
有极小值点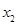 ,有极大值点
,有极大值点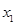 . ………8分
. ………8分综上所述, 当
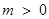 时,
时,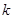 取任何实数, 函数
取任何实数, 函数 有极小值点
有极小值点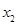 ;
;当
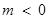 时,
时,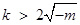 ,函数
,函数 有极小值点
有极小值点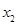 ,有极大值点
,有极大值点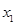 .…9分
.…9分(其中
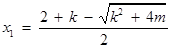 ,
, 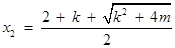 )
)(3)∵
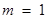 , ∴
, ∴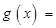
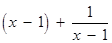 .
.∴
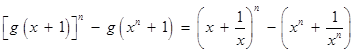
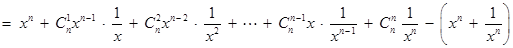
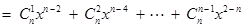 . ………10分
. ………10分令
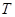
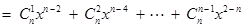 ,
,则
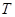
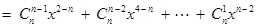
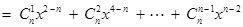 .
.∵
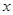
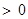 ,
,∴
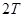
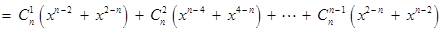 …11分
…11分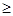
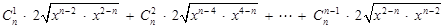 12分
12分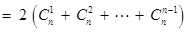
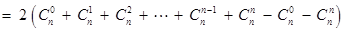
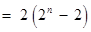 .………13分
.………13分∴
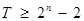 ,即
,即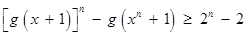 . ……………14分
. ……………14分证法2:下面用数学归纳法证明不等式
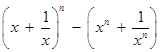
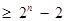 .
.① 当
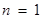 时,左边
时,左边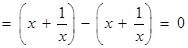 ,右边
,右边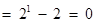 ,不等式成立;
,不等式成立;………10分
②假设当
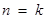
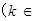 N
N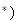 时,不等式成立,即
时,不等式成立,即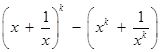
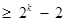 ,
,则
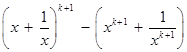
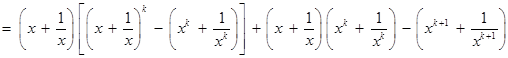
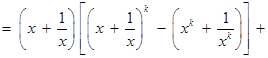
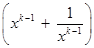 ………11分
………11分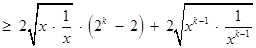 ………12分
………12分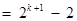 . ………13分
. ………13分也就是说,当
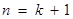 时,不等式也成立.
时,不等式也成立.由①②可得,对
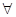
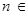 N
N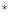 ,
,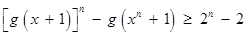 都成立. …14分
都成立. …14分
练习册系列答案
 口算题卡加应用题集训系列答案
口算题卡加应用题集训系列答案
相关题目
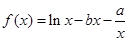 (
(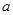 、
、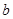 为常数),在
为常数),在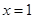 时取得极值.
时取得极值.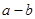 的值;
的值;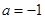 时,求函数
时,求函数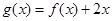 的最小值;
的最小值;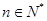 时,试比较
时,试比较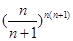 与
与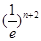 的大小并证明.
的大小并证明.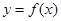 ,满足
,满足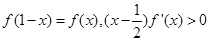 ,若
,若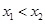 且
且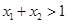 ,则有( )
,则有( )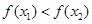
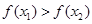
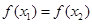
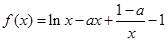 .
.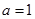 时,求曲线
时,求曲线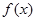 在
在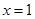 处的切线方程;
处的切线方程;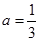 时,求函数
时,求函数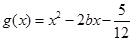 ,若对于
,若对于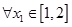 ,
,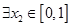 ,使
,使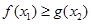 成立,求实数
成立,求实数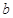 的取值范围.
的取值范围. 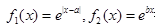
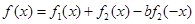 ,是否存在a,b
,是否存在a,b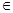 R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;
R,y=f(x)为偶函数.如果存在.请举例并证明你的结论,如果不存在,请说明理由;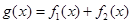 在R上的单调区间;
在R上的单调区间;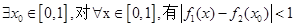 成立.求a的取值范围.
成立.求a的取值范围.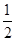 ax2+bx(a≠0),设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q,过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N,问是否存在点R,使C1在点M处的切线与C2在点N处的切线互相平行?若存在,求出点R的横坐标;若不存在,请说明理由.
ax2+bx(a≠0),设函数f(x)的图象C1与函数g(x)的图象C2交于两点P、Q,过线段PQ的中点R作x轴垂线分别交C1、C2于点M、N,问是否存在点R,使C1在点M处的切线与C2在点N处的切线互相平行?若存在,求出点R的横坐标;若不存在,请说明理由.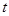 的函数
的函数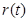 ,若球的体积以均匀速度
,若球的体积以均匀速度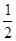 增长,则球的表面积的增长速度与球半径的乘积为 .
增长,则球的表面积的增长速度与球半径的乘积为 .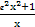 ,g(x)=
,g(x)=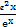 ,对任意x1,x2∈(0,+∞),不等式
,对任意x1,x2∈(0,+∞),不等式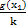 ≤
≤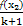 恒成立,则正数k的取值范围是 .
恒成立,则正数k的取值范围是 .