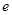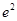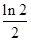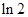题目内容
已知函数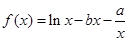 (
(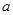 、
、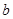 为常数),在
为常数),在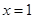 时取得极值.
时取得极值.
(1)求实数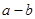 的值;
的值;
(2)当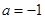 时,求函数
时,求函数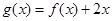 的最小值;
的最小值;
(3)当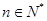 时,试比较
时,试比较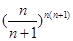 与
与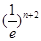 的大小并证明.
的大小并证明.
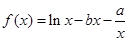 (
(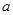 、
、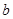 为常数),在
为常数),在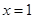 时取得极值.
时取得极值.(1)求实数
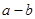 的值;
的值;(2)当
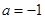 时,求函数
时,求函数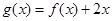 的最小值;
的最小值;(3)当
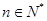 时,试比较
时,试比较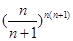 与
与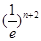 的大小并证明.
的大小并证明.(1)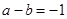 ;(2)
;(2)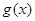 取最小值
取最小值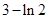 ;(3)
;(3)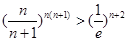 .
.
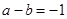 ;(2)
;(2)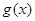 取最小值
取最小值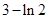 ;(3)
;(3)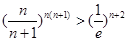 .
.试题分析:(1)因为函数
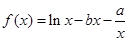 (
(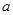 、
、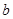 为常数),在
为常数),在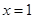 时取得极值,故
时取得极值,故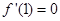 ,因此,先对函数
,因此,先对函数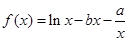 求导得,
求导得,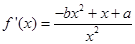 ,由
,由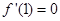 可得实数
可得实数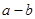 的值;(2)当
的值;(2)当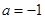 时,求函数
时,求函数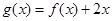 的最小值,当
的最小值,当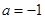 时,由
时,由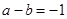 得
得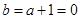 ,代入得
,代入得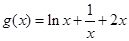
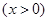 ,对
,对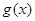 求导,判断单调性,即可得函数
求导,判断单调性,即可得函数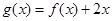 的最小值;(3)比较
的最小值;(3)比较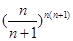 与
与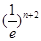 的大小,直接比较不好比较,可比较对数的大小即
的大小,直接比较不好比较,可比较对数的大小即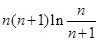 与
与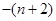 ,两式作差得
,两式作差得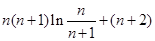 ,只需判断它的符号,即判断
,只需判断它的符号,即判断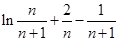 的符号,即判断
的符号,即判断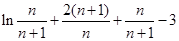 的符号,可构造函数
的符号,可构造函数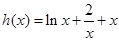 ,证明
,证明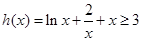 即可.
即可.试题解析:(1)
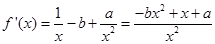
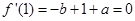
∴
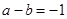 (3分)
(3分)(2)
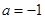 时
时 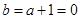
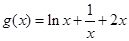
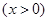 ,
,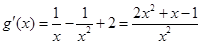
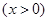
∴
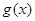 在
在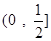 上单调递减,在
上单调递减,在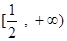 上单调递增 (6分)
上单调递增 (6分)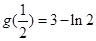
∴当
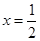 时,
时,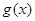 取最小值
取最小值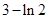 (8分)
(8分)(3)令
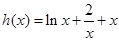
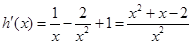
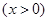 ,∴
,∴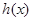 在
在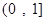 上单调递减,在
上单调递减,在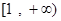 上单调递增
上单调递增 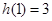 ,∴
,∴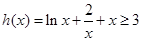 当且仅当
当且仅当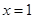 时取最小值
时取最小值∵
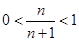 ∴
∴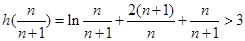
∴
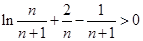 ∴
∴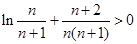
∴
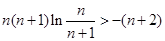 ∴
∴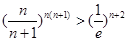 (14分)
(14分)
练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
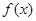 ,当
,当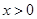 时,
时,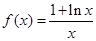 .
.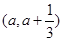
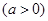 上存在极值点,求实数a的取值范围;
上存在极值点,求实数a的取值范围;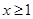 时,不等式
时,不等式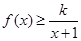 恒成立,求实数k的取值范围;
恒成立,求实数k的取值范围;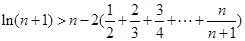
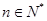 .
.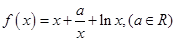 ,
,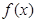 有最值,求实数
有最值,求实数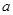 的取值范围;
的取值范围;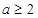 时,若存在
时,若存在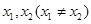 ,使得曲线
,使得曲线 在
在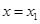 与
与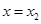 处的切线互相平行,求证
处的切线互相平行,求证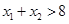 。
。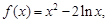
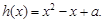
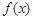 的极值;
的极值;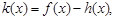 若函数
若函数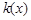 在
在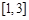 上恰有两个不同零点,求实数
上恰有两个不同零点,求实数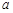 的取值范围.
的取值范围.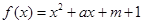 ,关于x的不等式
,关于x的不等式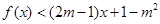 的解集为
的解集为 ,其中m为非零常数.设
,其中m为非零常数.设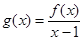 .
.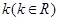 如何取值时,函数
如何取值时,函数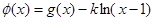 存在极值点,并求出极值点;
存在极值点,并求出极值点;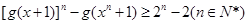
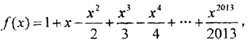 设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b
设函数F(x)= f(x+4),且F(x)的零点均在区间[a,b](a<b,a,b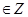 ) 内,,则x2+y2=b-a的面积的最小值为( )
) 内,,则x2+y2=b-a的面积的最小值为( )
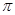
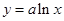
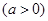 在
在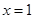 处的切线与两坐标轴围成的三角形的面积为4,则
处的切线与两坐标轴围成的三角形的面积为4,则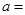 .
.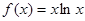 ,若
,若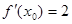 ,则
,则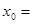 ( )
( )