题目内容
16. 如图,四棱锥E-ABCD中,面EBA⊥面ABCD,侧面ABE是等腰直角三角形,EA=EB,AB∥CD,AB⊥BC,AB=2CD=2BC=2.
如图,四棱锥E-ABCD中,面EBA⊥面ABCD,侧面ABE是等腰直角三角形,EA=EB,AB∥CD,AB⊥BC,AB=2CD=2BC=2.(Ⅰ)求证:AB⊥ED;
(Ⅱ)求直线CE与面ABE的所成角的正弦值.
分析 (Ⅰ)作EM⊥AB,交AB于M,连结DM,由已知得四边形BCDM是边长为1的正方形,由此能证明AB⊥ED.
(Ⅱ)由已知得BC⊥面ABE,直线CE与面ABE所成角为∠CEB,由此能求出直线CE与面ABE的所成角的正弦值.
解答 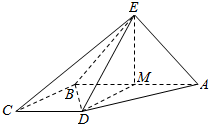 (Ⅰ)证明:作EM⊥AB,交AB于M,连结DM,
(Ⅰ)证明:作EM⊥AB,交AB于M,连结DM,
∵△ABE为等腰直角三角形,
∴M为AB的中点,
∵AB=2CD=2BC=2,AB∥CD,AB⊥BC,
∴四边形BCDM是边长为1的正方形,
∴AB⊥DM,
∵EM∩DM=M,
∴AB⊥面DEM,∴AB⊥ED.
(Ⅱ)解:∵AB⊥BC,面ABE⊥面ABCD,面ABE∩平面ABCD=AB,
∴BC⊥面ABE,直线CE与面ABE所成角为∠CEB,
∵BC=1,BE=$\sqrt{2}$,
∴CE=$\sqrt{3}$,∴sin∠CEB=$\frac{\sqrt{3}}{3}$.
点评 本题考查异面直线垂直的证明,考查直线与平面所成角的正弦值的求法,解题时要认真审题,注意空间思维能力的培养.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
4.假设关于某设备的使用年限x和所支出的维修费用y(万元)有如下的统计资料:
若由资料知y对x成线性相关关系、试求:
(1)线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的回归系数$\stackrel{∧}{b}$与$\stackrel{∧}{a}$
(2)估计使用年限为10年时,维修费用是多少?(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$)
| 使用年限x | 2 | 3 | 4 | 5 | 6 |
| 维修费用y | 2.2 | 3.8 | 5.5 | 6.5 | 7.0 |
(1)线性回归方程$\stackrel{∧}{y}$=$\stackrel{∧}{b}$x+$\stackrel{∧}{a}$的回归系数$\stackrel{∧}{b}$与$\stackrel{∧}{a}$
(2)估计使用年限为10年时,维修费用是多少?(参考公式:$\stackrel{∧}{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{i}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{{x}_{i}}^{2}-n{\overline{x}}^{2}}$)
5.设i是虚数单位,若$\frac{z}{2-i}$=1+i,则复数z=( )
| A. | 2+i | B. | 1+i | C. | 3+i | D. | 3=i |
6.已知数列{an}中,a1=1,a2=1,an+2=an+an+1,则a5=( )
| A. | 0 | B. | 3 | C. | 5 | D. | 8 |
