题目内容

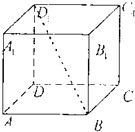
将图合成一个正方体后，直线PR与QR所成角的余弦是（　　）
A．0B．
1
5
C．-
1
5
D．-
1
2

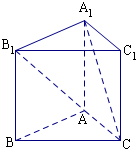
将图形还原成正方体，如图所示
设正方体的棱长为2，可得PR=RQ=
22+12
=
5

∵PQ为正方体的对角线，∴PQ=2
3

则△PQR中，由余弦定理得
cos∠PRQ=
PR2+QR2-PQ2
2PR•QR
=
5+5-12
2×
5
×
5
=-
1
5

∵直线PR与QR所成角为锐角或直角
∴PR与QR所成角的余弦等于|cos∠PRQ|=
1
5

故选：B
练习册系列答案
相关题目
如图，三棱锥P-ABC中，PA⊥平面ABC，△ABC是等边三角形，E是BC中点，若PA=AB，则异面直线PE与AB所成角的余弦值（　　）
A．
3
7
14
B．
21
6
C．
5
10
D．
2
3
如图，四面体ABCD中，O、E分别是BD、BC的中点，AO⊥平面BCD，CA=CB=CD=BD=2．
（1）求证：面ABD⊥面AOC；
（2）求异面直线AE与CD所成角的大小．
如图正方体ABCD-A1B1C1D1中，E，F分别为AB，CC1的中点，则异面直线A1C与EF所成角的余弦值为（　　）
A．
3
3
B．
2
3
C．
1
3
D．
1
6
如图，直三棱柱ABC-A1B1C1，AC⊥BC，且CA=CC1=2CB，则直线BC1与直线AB1所成角的余弦值为（　　）
A．
5
5
B．
5
3
C．
2
5
5
D．
3
5
正方体ABCD-A1B1C1D1中，异面直线AC与BD1所成角为______．
如图，已知正三棱柱ABC-A1B1C1的各条棱长都相等，则异面直线AB1和A1C所成的角的余弦值大小是______．
在△ABC中，AB=15，∠BCA=120°．若△ABC所在平面α外一点P到A、B、C的距离都是14，则直线PC与平面ABC所成角的正弦值为（　　）
A．
13
14
B．
11
14
C．
9
14
D．
1
2
如图，四棱锥S-ABCD的底面为正方形，SD⊥平面ABCD，SD=AD=2，请建立空间直角坐标系解决下列问题．
（1）求证：AC⊥SB；
（2）求直线SB与平面ADS所成角的正弦值．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网