题目内容
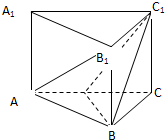
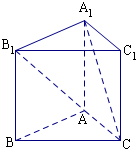
如图,在正方体ABCD-A1B1C1D1中,E、F分别是BB1、CD的中点
(1)证明:AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明:面AED⊥面A1FD1.

(1)证明:AD⊥D1F;
(2)求AE与D1F所成的角;
(3)证明:面AED⊥面A1FD1.

(1)∵AC1是正方体
∴AD⊥面DC1,
又D1F?面DC1,
∴AD⊥D1F
(2)取AB中点G,连接A1G,FG,
∵F是CD中点
∴GF
AD又A1D1
AD
∴GF
A1D1∴GFD1A1是平行四边形∴A1G∥D1F设A1G∩AE=H
则∠AHA1是AE与D1F所成的角
∵E是BB1的中点∴Rt△A1AG≌Rt△ABE
∴∠GA1A=∠GAH∴∠A1HA=90°即直线AE与D1F所成角是直角
(3)∵AD⊥D1F((1)中已证)
AE⊥D1F,又AD∩AE=A,∴D1F⊥面AED,又∵D1F?面A1FD1,
∴面AED⊥面A1FD1
∴AD⊥面DC1,
又D1F?面DC1,
∴AD⊥D1F
(2)取AB中点G,连接A1G,FG,
∵F是CD中点
∴GF
| ||
| . |
| ||
| . |
∴GF
| ||
| . |
则∠AHA1是AE与D1F所成的角
∵E是BB1的中点∴Rt△A1AG≌Rt△ABE
∴∠GA1A=∠GAH∴∠A1HA=90°即直线AE与D1F所成角是直角
(3)∵AD⊥D1F((1)中已证)
AE⊥D1F,又AD∩AE=A,∴D1F⊥面AED,又∵D1F?面A1FD1,
∴面AED⊥面A1FD1

练习册系列答案
相关题目