题目内容
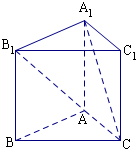
如图,在直三棱柱ABC-A1B1C1中,AC⊥BC,AC=BC=CC1,M为AB的中点.
(1)求证:BC1∥平面MA1C;
(2)求直线BC1与平面AA1B1B所成角的大小.
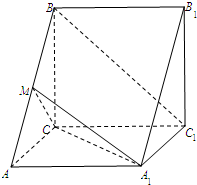
(1)求证:BC1∥平面MA1C;
(2)求直线BC1与平面AA1B1B所成角的大小.

(1)连接AC1,交A1C于O点,连接OM
∵三棱柱ABC-A1B1C1是直三棱柱
∴四边形AA1C1C是矩形,可得AO=OC1
∵M为AB的中点,
∴OM是△A1CB的中位线,可得OM∥BC1,
又∵OM?平面MA1C,BC1?平面MA1C
∴BC1∥平面MA1C;
(2)根据直三棱柱ABC-A1B1C1中AC⊥BC,可得CA、CB、CC1两两垂直,
因此以C为原点,CA、CC1、CB分别为x、y、z轴建立如图空间直角坐标系
设AC=1,可得C(0,0,0),A(1,0,0),A1(1,1,0),C1(0,1,0),B(0,0,1),
设平面AA1B1B的一个法向量为
=(x,y,z),直线BC1与平面AA1B1B所成角是α
∵
=(0,1,0),
=(-1,0,1),
∴可得方程组
,取x=1,得y=0,z=1
由此可得平面AA1B1B的法向量为
=(1,0,1),
∵
=(0,1,-1),
∴sinα=|cos<
,
>|=|
|=
∵直线BC1与平面AA1B1B所成角α是锐角
∴α=30°,即直线BC1与平面AA1B1B所成角为30°
∵三棱柱ABC-A1B1C1是直三棱柱
∴四边形AA1C1C是矩形,可得AO=OC1
∵M为AB的中点,
∴OM是△A1CB的中位线,可得OM∥BC1,
又∵OM?平面MA1C,BC1?平面MA1C
∴BC1∥平面MA1C;
(2)根据直三棱柱ABC-A1B1C1中AC⊥BC,可得CA、CB、CC1两两垂直,
因此以C为原点,CA、CC1、CB分别为x、y、z轴建立如图空间直角坐标系
设AC=1,可得C(0,0,0),A(1,0,0),A1(1,1,0),C1(0,1,0),B(0,0,1),
设平面AA1B1B的一个法向量为
| n |

∵
| AA1 |
| AB |
∴可得方程组
|
由此可得平面AA1B1B的法向量为
| n |
∵
| BC1 |
∴sinα=|cos<
| BC1 |
| n |
| ||||
|
|
| 1 |
| 2 |
∵直线BC1与平面AA1B1B所成角α是锐角
∴α=30°,即直线BC1与平面AA1B1B所成角为30°

练习册系列答案
 教材全解字词句篇系列答案
教材全解字词句篇系列答案
相关题目