题目内容
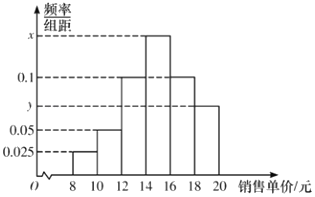
【题目】中国国际智能产业博览会（智博会）每年在重庆市举办一届，每年参加服务的志愿者分“嘉宾”、“法医”等若干小组，
年底，来自重庆大学、西南大学、重庆医科大学、西南政法大学的500名学生在重庆科技馆多功能厅参加了“志愿者培训”，如图是四所大学参加培训人数的不完整条形统计图，现用分层抽样的方法从中抽出20人作为2019年中国国际智博会服务的志愿者．
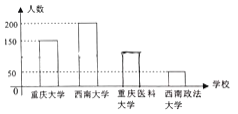
（1）分别求出从重庆大学、西南大学、重庆医科大学、西南政法大学抽出的志愿者人数；
（2）若“嘉宾”小组的2名志愿者只能从重庆医科大学或西南政法大学抽出，求这2人分别来自不同大学的概率（结果用分数表示）．
【答案】（1）6，8，4，2；（2）
．
【解析】
（1）根据分层抽样的特点，分别计算出所求的人数；（2）将全部的情况列出来，然后得到符合要求的情况，根据古典概型的公式，得到概率.
（1）由题意得：
从重庆大学、西南大学、重庆医科大学、西南政法大学抽出的志愿者人数分别为：
人，
人，
人，
人．
（2）设重庆医科大学的四名志愿者分别为
，
，
，
，
西南政法大学的两名志愿者分别为
，
则共有：
，
，
，
，
，
，
，
，
，
，
，
，
，
，
，共15种情况，
其中分别来自不同大学的有：，，，，，，，，共8种情况，
所以，这2人分别来自不同大学的概率为：
．
【题目】自由购是通过自助结算方式购物的一种形式.某大型超市为调查顾客使用自由购的情况，随机抽取了100人，统计结果整理如下：
20以下 | [20,30) | [30,40) | [40,50) | [50,60) | [60,70] | 70以上 | |
使用人数 | 3 | 12 | 17 | 6 | 4 | 2 | 0 |
未使用人数 | 0 | 0 | 3 | 14 | 36 | 3 | 0 |
（Ⅰ）现随机抽取1名顾客，试估计该顾客年龄在
且未使用自由购的概率；
（Ⅱ）从被抽取的年龄在
使用自由购的顾客中，随机抽取3人进一步了解情况，用
表示这3人中年龄在
的人数,求随机变量的分布列及数学期望；
（Ⅲ）为鼓励顾客使用自由购，该超市拟对使用自由购的顾客赠送1个环保购物袋.若某日该超市预计有5000人购物，试估计该超市当天至少应准备多少个环保购物袋.
