��Ŀ����
����Ŀ���躯��y=f��x��ͼ���ϲ�ͬ����A��x1 �� y1����B��x2 �� y2���������ߵ�б�ʷֱ���kA �� kB �� �涨�գ�A��B��= ![]() ��|AB|Ϊ�߶�AB�ij��ȣ���������y=f��x���ڵ�A���B֮��ġ������ȡ��������������⣺ �ٺ���y=x3ͼ��������A��B�ĺ�����ֱ�Ϊ1�ͩ�1����գ�A��B��=0��
��|AB|Ϊ�߶�AB�ij��ȣ���������y=f��x���ڵ�A���B֮��ġ������ȡ��������������⣺ �ٺ���y=x3ͼ��������A��B�ĺ�����ֱ�Ϊ1�ͩ�1����գ�A��B��=0��
�ڴ��������ĺ�����ͼ������������֮��ġ������ȡ�Ϊ������
�����A��B��������y=x2+1�ϲ�ͬ�����㣬��գ�A��B����2��
��������y=ex��e����Ȼ�����ĵ������ϲ�ͬ����A��x1 �� y1����B��x2 �� y2������գ�A��B����1��
��������������Ϊ �� �����������������Ŷ����ϣ�
���𰸡��٢ڢۢ�
���������⣺���ڢ٣���y=x3����y��=3x2��
��kA=3��kB=3����|kA��kB|=0����գ�A��B��=0���ʢ���ȷ��
���ڢڣ���y=1ʱ��y��=0����գ�A��B��=0���ʢ���ȷ��
���ڢۣ�������y=x2+1�ĵ���Ϊy��=2x��yA=xA2+1��yB=xB2+1��
yA��yB=xA2��xB2=��xA��xB����xA+xB����
��գ�A��B��= ![]() =
= ![]() =
= ![]() ��2���ʢ���ȷ��
��2���ʢ���ȷ��
���ڢܣ���y=ex����y��=ex���գ�A��B��= 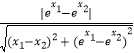 ��
��
�ɲ�ͬ����A��x1��y1����B��x2��y2�����ɵæգ�A��B���� 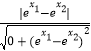 =1��
=1��
�ʢ���ȷ��
���Դ��ǣ��٢ڢۢ�
�����㾫����������Ŀ����֪�������������������ж���Ӧ�õ����֪ʶ���Եõ�����Ĵ𰸣���Ҫ�����������⻥Ϊ������⣬��������ͬ������ԣ���������Ϊ������������⣬���ǵ������û�й�ϵ��

 ����ѵ��ϵ�д�
����ѵ��ϵ�д� ��ĩ�����ϵ�д�
��ĩ�����ϵ�д�