题目内容
F1,F2是 的左、右焦点,点P在椭圆上运动,则
的左、右焦点,点P在椭圆上运动,则 的最大值是
的最大值是
 的左、右焦点,点P在椭圆上运动,则
的左、右焦点,点P在椭圆上运动,则 的最大值是
的最大值是| A.4 | B.5 | C.2 | D.1 |
A
分析:
 =(a-ex)(a+ex)=a2-e2x2,由此可求出
=(a-ex)(a+ex)=a2-e2x2,由此可求出 的最大值.
的最大值.解:由焦半径公式
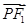 =a-ex,
=a-ex,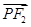 =a+ex
=a+ex =(a-ex)(a+ex)=a2-e2x2
=(a-ex)(a+ex)=a2-e2x2则
 的最大值是a2=4.
的最大值是a2=4.答案:A.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
题目内容
 的左、右焦点,点P在椭圆上运动,则
的左、右焦点,点P在椭圆上运动,则 的最大值是
的最大值是| A.4 | B.5 | C.2 | D.1 |
 =(a-ex)(a+ex)=a2-e2x2,由此可求出
=(a-ex)(a+ex)=a2-e2x2,由此可求出 的最大值.
的最大值.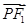 =a-ex,
=a-ex,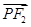 =a+ex
=a+ex =(a-ex)(a+ex)=a2-e2x2
=(a-ex)(a+ex)=a2-e2x2 的最大值是a2=4.
的最大值是a2=4.
 阅读快车系列答案
阅读快车系列答案