题目内容
已知等比数列{an},前n项和为Sn=3n+c,其中c是常数,则数列通项an= .
考点:等比数列的通项公式
专题:等差数列与等比数列
分析:根据当n=1时a1=S1,当n≥2时an=Sn-Sn-1,把条件代入化简求出an.
解答:
解:当n=1时,a1=S1=3+c,
当n≥2时,an=Sn-Sn-1=3n+c-(3n-1+c)=2•3n-1,
因为数列{an}是等比数列,
所以当n=1时也满足上式,则3+c=2,得c=-1,
所以an=2•3n-1,
故答案为:2•3n-1.
当n≥2时,an=Sn-Sn-1=3n+c-(3n-1+c)=2•3n-1,
因为数列{an}是等比数列,
所以当n=1时也满足上式,则3+c=2,得c=-1,
所以an=2•3n-1,
故答案为:2•3n-1.
点评:本题考查数列中an与Sn的关系式应用,以及等比数列的通项公式,属于基础题.

练习册系列答案
相关题目
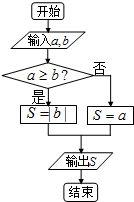 定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )
定义某种运算⊕,a⊕b的运算原理如图所示,设S=1⊕x,x∈[-2,2],则输出的S的最大值与最小值的差为( )| A、2 | B、-1 | C、4 | D、3 |
函数y=x2-1的值域是( )
| A、[-1,+∞) |
| B、R |
| C、[0,+∞) |
| D、[1,+∞) |
直线y=2x+1与y轴的交点所组成的集合为( )
| A、{0,1} | ||
| B、{(0,1)} | ||
C、{-
| ||
D、{(-
|
P:x≥3或x≤1,Q:x2-3x+2≥0,则“非P”是“非Q”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知集合A={y|y=log3x,x>1},B={y|y=(
)x,x>1},则A∩B=( )
| 1 |
| 3 |
A、{y |0<y<
| ||
| B、{y|0<y<1} | ||
C、{y |
| ||
| D、∅ |