题目内容
已知数列{an},对于n∈N+,点P(n,an)始终在函数f(x)=-2x+5的图象上,
(Ⅰ)求证:数列{an}是等差数列.
(Ⅱ)求数列{an}前n项和Sn的最大值.
(Ⅰ)求证:数列{an}是等差数列.
(Ⅱ)求数列{an}前n项和Sn的最大值.
考点:等差数列的前n项和,等差数列的性质
专题:等差数列与等比数列
分析:(Ⅰ)由已知得an=-2n+5,从而a1=-2+5=3,an+1-an=-2(n+1)+5-(-2n+5)=-2,由此能证明数列{an}是首项为3,公差为-2的等差数列.
(Ⅱ)由已知得Sn=3n+
×(-2)=-n2+4n=-(n-2)2+4,由此能求出数列{an}前n项和Sn的最大值.
(Ⅱ)由已知得Sn=3n+
| n(n-1) |
| 2 |
解答:
(Ⅰ)证明:∵数列{an},对于n∈N+,
点P(n,an)始终在函数f(x)=-2x+5的图象上,
∴an=-2n+5,
∴a1=-2+5=3,
an+1-an=-2(n+1)+5-(-2n+5)=-2,
∴数列{an}是首项为3,公差为-2的等差数列.
(Ⅱ)解:∵数列{an}是首项为3,公差为-2的等差数列,
∴Sn=3n+
×(-2)
=-n2+4n=-(n-2)2+4,
∴n=2时,数列{an}前n项和Sn取最大值4.
点P(n,an)始终在函数f(x)=-2x+5的图象上,
∴an=-2n+5,
∴a1=-2+5=3,
an+1-an=-2(n+1)+5-(-2n+5)=-2,
∴数列{an}是首项为3,公差为-2的等差数列.
(Ⅱ)解:∵数列{an}是首项为3,公差为-2的等差数列,
∴Sn=3n+
| n(n-1) |
| 2 |
=-n2+4n=-(n-2)2+4,
∴n=2时,数列{an}前n项和Sn取最大值4.
点评:本题考查等差数列的证明,考查等差数列的前n项和的最大值的求法,是基础题,解题时要注意等差数列的性质的合理运用.

练习册系列答案
 初中学业考试导与练系列答案
初中学业考试导与练系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
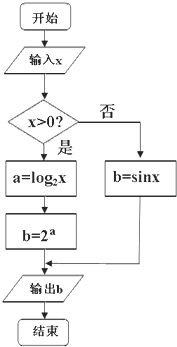 如图所示的程序框图,若两次输入的x值分别是3π和-
如图所示的程序框图,若两次输入的x值分别是3π和-| π |
| 3 |
A、1,
| ||||
B、0,
| ||||
C、-π,-
| ||||
D、3π,-
|
下列函数中,二次函数是( )
| A、y=8x2+1 | ||
| B、y=8x+1 | ||
C、y=
| ||
D、y=
|
一个物体的运动方程为s=-
t3+2t2-5,其中s的单位是米,t的单位是秒,那么物体在3秒末的瞬时速度是( )
| 1 |
| 3 |
| A、3米/秒 | B、6米/秒 |
| C、5米/秒 | D、4米/秒 |
在△ABC中,角A,B,C的对边长分别为a,b,c,a=8,B=60°,C=75°,则b=( )
A、4
| ||
B、4
| ||
C、4
| ||
D、
|
若集合M={a,b,c},N={x|x⊆M},则下列关系正确的是( )
| A、M∈N | B、N⊆M |
| C、M⊆N | D、M=N |
非零实数x、y、z成等差数列,x+1、y、z与x、y、z+2均成等比数列,则y等于( )
| A、16 | B、14 | C、12 | D、10 |