题目内容
(1)求过点M(2,-1)且与圆x2+y2-2x+10y=0同心的圆C的方程,
(2)求圆C过点M的切线方程.
(2)求圆C过点M的切线方程.
考点:圆的切线方程,圆的一般方程
专题:直线与圆
分析:(1)求出圆C的圆心与半径,写出圆C的标准方程;
(2)求出直线CM的斜率,得出过点M的切线斜率,利用点斜式写出所求的切线方程.
(2)求出直线CM的斜率,得出过点M的切线斜率,利用点斜式写出所求的切线方程.
解答:
解:(1)圆x2+y2-2x+10y=0可化为:
(x-1)2+(y+5)2=26,
∴圆心为(1,-5),
即圆C的圆心为(1,-5);…(2分)
又∵圆C过点M(2,-1),
∴圆C的半径r=|CM|=
=
;…(4分)
∴所求圆的方程为(x-1)2+(y+5)2=17;…(7分)
(2)∵M(2,-1)在圆上,
∴过点M的切线有一条;
又∵直线CM的斜率是kCM=
=4,
∴过点M的切线的斜率为k =-
,…(10分)
∴所求的切线方程为y+1=-
(x-2),
即x+4y+2=0.…(14分)
(x-1)2+(y+5)2=26,
∴圆心为(1,-5),
即圆C的圆心为(1,-5);…(2分)
又∵圆C过点M(2,-1),
∴圆C的半径r=|CM|=
| (2-1)2+(-1+5)2 |
| 17 |
∴所求圆的方程为(x-1)2+(y+5)2=17;…(7分)
(2)∵M(2,-1)在圆上,
∴过点M的切线有一条;
又∵直线CM的斜率是kCM=
| -1+5 |
| 2-1 |
∴过点M的切线的斜率为k =-
| 1 |
| 4 |
∴所求的切线方程为y+1=-
| 1 |
| 4 |
即x+4y+2=0.…(14分)
点评:本题考查了直线与圆的应用问题,考查了求圆的标准方程以及圆的切线方程的应用问题,是基础题.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
已知双曲线
-
=1的一条渐近线方程为y=
x,则双曲线的离心率为( )
| x2 |
| a2 |
| y2 |
| b2 |
| 4 |
| 3 |
A、
| ||
B、
| ||
C、
| ||
D、
|
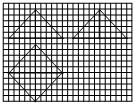 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为