题目内容
P:x≥3或x≤1,Q:x2-3x+2≥0,则“非P”是“非Q”的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
考点:必要条件、充分条件与充要条件的判断
专题:简易逻辑
分析:根据不等式的关系,结合充分条件和必要条件的定义即可得到结论.
解答:
解:由x2-3x+2≥0,得x≥2或x≤1,则Q:x≥2或x≤1,非Q:1<x<2,
非P:1<x<3,
则“非P”是“非Q”的必要不充分条件,
故选:B
非P:1<x<3,
则“非P”是“非Q”的必要不充分条件,
故选:B
点评:本题主要考查充分条件和必要条件的判断,比较基础.

练习册系列答案
 状元坊全程突破导练测系列答案
状元坊全程突破导练测系列答案
相关题目
若集合M={a,b,c},N={x|x⊆M},则下列关系正确的是( )
| A、M∈N | B、N⊆M |
| C、M⊆N | D、M=N |
设a>0,b>0且a+b=1则
+
的最小值是( )
| 1 |
| a |
| 2 |
| b |
| A、2 | ||
| B、4 | ||
C、3+2
| ||
| D、6 |
若定义在R上的奇函数f(x)满足f(x-4)=-f(x),且在区间[0,2]上是增函数,则有( )
| A、f(-25)<f(80)<f(11) |
| B、f(11)<f(80)<f(-25) |
| C、f(-25)<f(11)<f(80) |
| D、f(80)<f(11)<f(-25) |
“x=-2”是“x≠0”的( )
| A、充分而不必要条件 |
| B、必要而不充分条件 |
| C、充分必要条件 |
| D、既不充分也不必要条件 |
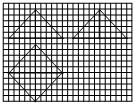 一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为
一个几何体的三视图如图所示,其中网格纸上的小正方形的边长为1,则该几何体的体积为