题目内容
已知数列{an}时公差不为零的等差数列,a1=1,a1,a3,a9成等比数列,则数列{an•2an}的前n项和sn=______.
∵a1=1,a1,a3,a9成等比数列,
∴a1a9=
,
即1+8d=(1+2d)2,
∴4d=4d2,
解得d=1,
∴an=1+n-1=n,an•2an=n•2n,
则sn=1?2+2?22+???+n?2n ①,
2Sn=1?22+2?23+???+n?2n+1,②,
两式相减得:
-Sn=2+22+???+2n-n?2n+1=
-n?2n+1=(1-n)?2n+1-2,
即Sn=(n-1)?2n+1+2,
故答案为:(n-1)?2n+1+2.
∴a1a9=
| a | 23 |
即1+8d=(1+2d)2,
∴4d=4d2,
解得d=1,
∴an=1+n-1=n,an•2an=n•2n,
则sn=1?2+2?22+???+n?2n ①,
2Sn=1?22+2?23+???+n?2n+1,②,
两式相减得:
-Sn=2+22+???+2n-n?2n+1=
| 2(1-2n) |
| 1-2 |
即Sn=(n-1)?2n+1+2,
故答案为:(n-1)?2n+1+2.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目

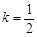 时,数列{an}为递减数列;
时,数列{an}为递减数列;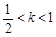 时,数列{an}不一定有最大项;
时,数列{an}不一定有最大项;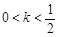 时,数列{an}为递减数列;
时,数列{an}为递减数列;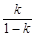 为正整数时,数列{an}必有两项相等的最大项.
为正整数时,数列{an}必有两项相等的最大项.