题目内容
4.已知函数f(x)=-x2+2ax-a.(1)若g(x)=f(x)+3x是偶函数,求a的值;
(2)若函数f(x)≤2在[1,+∞)上恒成立,求a的取值范围.
分析 (1)利用偶函数的图象关于y轴对称,建立方程,即可求a的值;
(2)确定函数的对称轴,分类讨论,求出函数f(x)的最大值,利用函数f(x)≤2在[1,+∞)上恒成立,即可求a的取值范围.
解答 解:(1)g(x)=-x2+(2a+3)x-a,
∵g(x)=f(x)+3x是偶函数,
∴2a+3=0,
∴a=-$\frac{3}{2}$;
(2)∵f(x)=-x2+2ax-a=-(x-a)2-a+a2,
∴函数f(x)的对称轴是x=a,
①a≤1时,f(x)max=f(1)=a-1,
∴只需a-1≤2即可,
∴a≤1,
②a>1时,f(x)max=f(a)=-a+a2,
∴只需-a+a2≤2即可,
∴1<a≤2,
综上,a≤2.
点评 本题考查函数的性质,考查恒成立问题,正确分类求最值是关键.

练习册系列答案
相关题目
15.在△ABC中,A=60°,若a,b,c成等比数列,则$\frac{bsinB}{c}$=( )
| A. | $\frac{1}{2}$ | B. | $\frac{\sqrt{2}}{2}$ | C. | $\frac{\sqrt{3}}{2}$ | D. | $\frac{\sqrt{6}+\sqrt{2}}{4}$ |
 如图,平面α,β,γ两两平行,且直线l与α,β,γ分别相交于点A,B,C,直线m与α,β,γ分别相交于点D,E,F,AB=6,BC=2,EF=3,求DE的长.
如图,平面α,β,γ两两平行,且直线l与α,β,γ分别相交于点A,B,C,直线m与α,β,γ分别相交于点D,E,F,AB=6,BC=2,EF=3,求DE的长.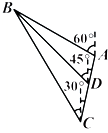 如图,已知一艘船以30海里/小时的速度往北偏东15°的A岛行驶,计划到A岛后再到B岛;B岛在A岛的北偏西60°的方向上,船到达C处时测得B岛在北偏西30°的方向,经过20分钟到达D处,测得B岛在北偏西45°的方向.
如图,已知一艘船以30海里/小时的速度往北偏东15°的A岛行驶,计划到A岛后再到B岛;B岛在A岛的北偏西60°的方向上,船到达C处时测得B岛在北偏西30°的方向,经过20分钟到达D处,测得B岛在北偏西45°的方向.