题目内容
【题目】在平面直角坐标系![]() 中,椭圆
中,椭圆![]() 的参数方程为
的参数方程为![]() (
(![]() 为参数).以坐标原点
为参数).以坐标原点![]() 为极点,
为极点,![]() 轴的正半轴为极轴建立极坐标系,直线
轴的正半轴为极轴建立极坐标系,直线![]() 的极坐标方程为
的极坐标方程为![]() .
.
(1)求椭圆![]() 的极坐标方程和直线
的极坐标方程和直线![]() 的直角坐标方程;
的直角坐标方程;
(2)若点![]() 的极坐标为
的极坐标为![]() ,直线
,直线![]() 与椭圆
与椭圆![]() 相交于
相交于![]() ,
,![]() 两点,求
两点,求![]() 的值.
的值.
【答案】(1)![]() ,
,![]() ;(2)
;(2)![]()
【解析】
(1)由椭圆![]() 的参数方程消参数
的参数方程消参数![]() 可得椭圆
可得椭圆![]() 的普通方程,再将
的普通方程,再将![]() 代入椭圆
代入椭圆![]() 的普通方程即可求得椭圆
的普通方程即可求得椭圆![]() 的极坐标方程,由
的极坐标方程,由![]() 即可将直线
即可将直线![]() 的极坐标方程化为直角坐标方程,问题得解。
的极坐标方程化为直角坐标方程,问题得解。
(2)求出点![]() 的直角坐标为
的直角坐标为![]() ,即可设直线
,即可设直线![]() 的参数方程为
的参数方程为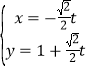 ,联立椭圆方程与直线参数方程,可得:
,联立椭圆方程与直线参数方程,可得:![]() ,
,![]() ,结合直线参数方程中参数的几何意义可得
,结合直线参数方程中参数的几何意义可得 ![]() ,问题得解。
,问题得解。
(1)椭圆![]() 的普通方程为
的普通方程为![]() ,
,
将![]() 代入整理得:
代入整理得:![]()
![]() 椭圆
椭圆![]() 的极坐标方程为
的极坐标方程为![]() ,
,
由![]() 得直线
得直线![]() 的直角坐标方程为:
的直角坐标方程为:![]() ;
;
(2)设点![]() ,
,![]() 对应的参数分别为
对应的参数分别为![]() ,
,![]() ,
,
点![]() 的直角坐标为:
的直角坐标为:![]() ,它在直线
,它在直线![]() 上.
上.
设直线![]() 的参数方程为
的参数方程为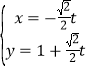 (
(![]() 为参数),
为参数),
代入![]() ,得
,得![]() ,
,
化简得![]() ,所以
,所以![]() ,
,![]()
由直线参数方程的几何意义可得:
![]() .
.

练习册系列答案
相关题目
【题目】某人有楼房一幢,室内总面积为![]() ,拟分割成两类房间作为旅游客房,有关的数据如下表:
,拟分割成两类房间作为旅游客房,有关的数据如下表:
大房间 | 小房间 | |
每间的面积 |
|
|
每间装修费 |
| 6000元 |
每天每间住人数 | 5人 | 3人 |
每天每人住宿费 | 80元 | 100元 |
如果他只能筹款80000元用于装修,且游客能住满客房,他应隔出大房间和小房间各多少间,能获得的住宿总收入最多?每天获得的住宿总收入最多是多少?
【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:
组号 | 分组 | 频率 |
第1组 |
|
|
第2组 |
|
|
第3组 |
|
|
第4组 |
|
|
第5组 |
|
|

![]() 求出频率分布表中
求出频率分布表中![]() 处应填写的数据,并完成如图所示的频率分布直方图;
处应填写的数据,并完成如图所示的频率分布直方图;
![]() 根据直方图估计这次自主招生考试笔试成绩的平均数和中位数
根据直方图估计这次自主招生考试笔试成绩的平均数和中位数![]() 结果都保留两位小数
结果都保留两位小数![]() .
.