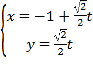题目内容
【题目】给出下列命题:
(1)直线![]() 与线段
与线段![]() 相交,其中
相交,其中![]() ,
,![]() ,则
,则![]() 的取值范围是
的取值范围是![]() ;
;
(2)点![]() 关于直线
关于直线![]() 的对称点为
的对称点为![]() ,则
,则![]() 的坐标为
的坐标为![]() ;
;
(3)圆![]() 上恰有
上恰有![]() 个点到直线
个点到直线![]() 的距离为
的距离为![]() ;
;
(4)直线![]() 与抛物线
与抛物线![]() 交于
交于![]() ,
,![]() 两点,则以
两点,则以![]() 为直径的圆恰好与直线
为直径的圆恰好与直线![]() 相切.
相切.
其中正确的命题有_________.(把所有正确的命题的序号都填上)
【答案】(2)(3)(4)
【解析】
根据两直线相交,点关于直线对称,直线与圆的位置关系,直线与抛物线的位置关系对各个命题进行判断.
(1)由于直线![]() 与线段AB有公共点,因此k的范围是
与线段AB有公共点,因此k的范围是![]() ,(1)错;
,(1)错;
(2)![]() 的中点坐标为
的中点坐标为![]() ,
,![]() ,即中点在直线
,即中点在直线![]() 上,又
上,又![]() ,直线
,直线![]() 的斜率是2,相乘等于
的斜率是2,相乘等于![]() ,
,![]() 与直线
与直线![]() 垂直,(2)正确;
垂直,(2)正确;
(3)圆心C到直线l的距离为1,圆半径为2,与直线l距离为1的两条直线一条与圆相交,一条与圆相切,因此圆上有![]() 个点到直线
个点到直线![]() 的距离为
的距离为![]() ,(3)正确;
,(3)正确;
(4)直线![]() 过抛物线的焦点F(1,0),直线
过抛物线的焦点F(1,0),直线![]() 是抛物线的准线,设
是抛物线的准线,设![]() ,由抛物线定义得
,由抛物线定义得![]() ,
,![]() 的中点
的中点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,∴以
,∴以![]() 为直径的圆恰好与直线
为直径的圆恰好与直线![]() 相切.(4)正确.
相切.(4)正确.
故答案为:(2)(3)(4).

练习册系列答案
 新课标同步训练系列答案
新课标同步训练系列答案 一线名师口算应用题天天练一本全系列答案
一线名师口算应用题天天练一本全系列答案
相关题目