题目内容
【题目】下列说法正确的是( )
A. 甲、乙二人比赛，甲胜的概率为
，则比赛5场，甲胜3场
B. 某医院治疗一种疾病的治愈率为10%，前9个病人没有治愈，则第10个病人一定治愈
C. 随机试验的频率与概率相等
D. 天气预报中，预报明天降水概率为90%，是指降水的可能性是90%
【答案】D
【解析】
概率表示事件发生的可能性的大小，具有随机性，频率代表实验中事件实际发生的次数与试验总次数之比，为实际值，由此判断即可.
A选项，此概率只说明发生的可能性大小，具有随机性，并非一定是5场胜3场；
B选项，此治愈率只说明发生的可能性大小，具有随机性，并非10人一定有人治愈；
C选项，试验的频率可以估计概率，并不等于概率；
D选项，概率为90%，即可能性为90%.
故选D.
名校课堂系列答案
【题目】某超市随机选取
位顾客，记录了他们购买甲、乙、丙、丁四种商品的情况，整理成如下统计表，其中“√”表示购买，“×”表示未购买．
| 甲 | 乙 | 丙 | 丁 |
| √ | × | √ | √ |
| × | √ | × | √ |
| √ | √ | √ | × |
| √ | × | √ | × |
85 | √ | × | × | × |
| × | √ | × | × |
（Ⅰ）估计顾客同时购买乙和丙的概率；
（Ⅱ）估计顾客在甲、乙、丙、丁中同时购买
中商品的概率；
（Ⅲ）如果顾客购买了甲，则该顾客同时购买乙、丙、丁中那种商品的可能性最大？
【题目】为了监控某种零件的一条生产线的生产过程，检验员每隔30 min从该生产线上随机抽取一个零件，并测量其尺寸（单位：cm）．下面是检验员在一天内依次抽取的16个零件的尺寸：
抽取次序 | 1 | 2 | 3 | 4 | 5 | 6 | 7 | 8 |
零件尺寸 | 9.95 | 10.12 | 9.96 | 9.96 | 10.01 | 9.92 | 9.98 | 10.04 |
抽取次序 | 9 | 10 | 11 | 12 | 13 | 14 | 15 | 16 |
零件尺寸 | 10.26 | 9.91 | 10.13 | 10.02 | 9.22 | 10.04 | 10.05 | 9.95 |
经计算得
， 
， 
， 
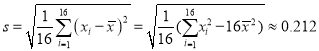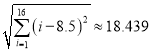，其中
为抽取的第
个零件的尺寸， 
．
（1）求
的相关系数
，并回答是否可以认为这一天生产的零件尺寸不随生产过程的进行而系统地变大或变小（若
，则可以认为零件的尺寸不随生产过程的进行而系统地变大或变小）．
（2）一天内抽检零件中，如果出现了尺寸在
之外的零件，就认为这条生产线在这一天的生产过程可能出现了异常情况，需对当天的生产过程进行检查．
（ⅰ）从这一天抽检的结果看，是否需对当天的生产过程进行检查？
（ⅱ）在
之外的数据称为离群值，试剔除离群值，估计这条生产线当天生产的零件尺寸的均值与标准差．（精确到0.01）
附：样本
的相关系数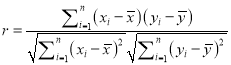
， 
．
