题目内容
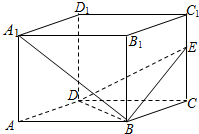
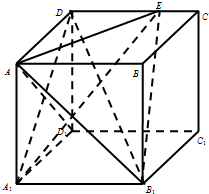
在长方体ABCD-A1B1C1D1中,AB=4,BC=2,CC1=3,
=2
(1)求点D1到平面BDE的距离;
(2)求直线A1B与平面BDE所成角的正弦值.
| CE |
| EC1 |
(1)求点D1到平面BDE的距离;
(2)求直线A1B与平面BDE所成角的正弦值.

(1)如图建立空间直角坐标系:
D(0,0,0),B(2,4,0),E(0,4,2),D1(0,0,3),
∴
=(2,4,0),
=(0,4,2),
=(0,0,3)
设面DBE的法向量为
=(x,y,z),
由
⇒
,
令y=1,则x=-2,z=-2.
=(-2,1,-2)d=|
|=|
|=2.
(2)A1(2,0,3),B(2,4,0),
=(0,4,-3)
设直线A1B与平面BDE所成的角为θ则sinθ=|cos<
,
>|=
=
=
.
所以直线A1B与平面BDE所成角的正弦值为
.
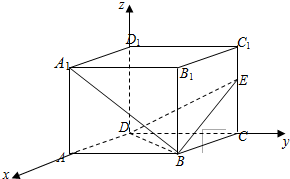
D(0,0,0),B(2,4,0),E(0,4,2),D1(0,0,3),
∴
| DB |
| DE |
| DD1 |
设面DBE的法向量为
| n |
由
|
|
令y=1,则x=-2,z=-2.
| n |
| ||||
|
|
| (0,0,3)•(-2,1,-2) |
| 3 |
(2)A1(2,0,3),B(2,4,0),
| A1B |
设直线A1B与平面BDE所成的角为θ则sinθ=|cos<
| A1B |
| n |
|
| ||||
|
|
| 10 |
| 5×3 |
| 2 |
| 3 |
所以直线A1B与平面BDE所成角的正弦值为
| 2 |
| 3 |


练习册系列答案
 浙江名校名师金卷系列答案
浙江名校名师金卷系列答案
相关题目
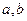 是两条异面直线,
是两条异面直线,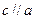 ,那么
,那么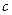 与
与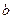 的位置关系____________________。
的位置关系____________________。