题目内容
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AB=4,BC=3,AD=5,∠DAB=∠ABC=90°,E是CD的中点.
(Ⅰ)证明:CD⊥平面PAE;
(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.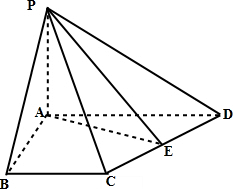
(Ⅰ)证明:CD⊥平面PAE;
(Ⅱ)若直线PB与平面PAE所成的角和PB与平面ABCD所成的角相等,求四棱锥P-ABCD的体积.

解法一:(Ⅰ)连接AC,由AB=4,BC=3,∠ABC=90°,得AC=5,
又AD=5,E是CD得中点,
所以CD⊥AE,
PA⊥平面ABCD,CD?平面ABCD.
所以PA⊥CD,
而PA,AE是平面PAE内的两条相交直线,
所以CD⊥平面PAE.
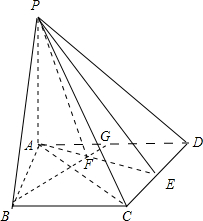
(Ⅱ)过点B作BG∥CD,分别与AE,AD相交于点F,G,连接PF,
由CD⊥平面PAE知,BG⊥平面PAE,于是∠BPF为直线PB与平面PAE所成的角,且BG⊥AE.
由PA⊥平面ABCD知,∠PBA即为直线PB与平面ABCD所成的角.
由题意∠PBA=∠BPF,因为sin∠PBA=
,sin∠BPF=
,所以PA=BF.
由∠DAB=∠ABC=90°知,AD∥BC,又BG∥CD.
所以四边形BCDG是平行四边形,
故GD=BC=3,于是AG=2.
在RT△BAG中,AB=4,AG=2,BG⊥AF,
所以BG=
=2
,BF=
=
=
.
于是PA=BF=
.
又梯形ABCD的面积为S=
×(5+3)×4=16.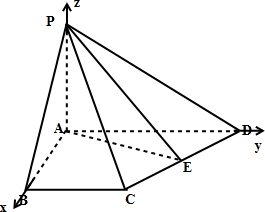
所以四棱锥P-ABCD的体积为V=
×S×PA=
×16×
=
.
解法二:以A为坐标原点,AB,AD,AP所在直线分别为X轴,Y轴,Z轴建立空间直角坐标系,
设PA=h,则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h).
(Ⅰ)
=(-4,2,0),
=(2,4,0),
=(0,0,h).
因为
•
=-8+8+0=0,
•
=0.
所以CD⊥AE,CD⊥AP,而AP,AE是平面PAE内的两条相交直线,
所以CD⊥平面PAE.
(Ⅱ)由题设和第一问知,
,
分别是平面PAE,平面ABCD的法向量,
而PB与平面PAE所成的角和PB与平面ABCD所成的角相等,
所以:|cos<
,
>|=|cos<
,
>|,即|
|=|
|.
由第一问知
=(-4,2,0),
=((0,0,-h),又
=(4,0,-h).
故|
|=|
|.
解得h=
.
又梯形ABCD的面积为S=
×(5+3)×4=16.
所以四棱锥P-ABCD的体积为V=
×S×PA=
×16×
=
.
又AD=5,E是CD得中点,
所以CD⊥AE,
PA⊥平面ABCD,CD?平面ABCD.
所以PA⊥CD,
而PA,AE是平面PAE内的两条相交直线,
所以CD⊥平面PAE.
(Ⅱ)过点B作BG∥CD,分别与AE,AD相交于点F,G,连接PF,
由CD⊥平面PAE知,BG⊥平面PAE,于是∠BPF为直线PB与平面PAE所成的角,且BG⊥AE.
由PA⊥平面ABCD知,∠PBA即为直线PB与平面ABCD所成的角.
由题意∠PBA=∠BPF,因为sin∠PBA=
| PA |
| PB |
| BF |
| PB |
由∠DAB=∠ABC=90°知,AD∥BC,又BG∥CD.
所以四边形BCDG是平行四边形,
故GD=BC=3,于是AG=2.
在RT△BAG中,AB=4,AG=2,BG⊥AF,
所以BG=
| AB2+AG2 |
| 5 |
| AB2 |
| BG |
| 16 | ||
2
|
8
| ||
| 5 |
于是PA=BF=
8
| ||
| 5 |
又梯形ABCD的面积为S=
| 1 |
| 2 |

所以四棱锥P-ABCD的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
8
| ||
| 5 |
128
| ||
| 15 |
解法二:以A为坐标原点,AB,AD,AP所在直线分别为X轴,Y轴,Z轴建立空间直角坐标系,
设PA=h,则A(0,0,0),B(4,0,0),C(4,3,0),D(0,5,0),E(2,4,0),P(0,0,h).
(Ⅰ)
| CD |
| AE |
| AP |
因为
| CD |
| AE |
| CD |
| AP |
所以CD⊥AE,CD⊥AP,而AP,AE是平面PAE内的两条相交直线,
所以CD⊥平面PAE.
(Ⅱ)由题设和第一问知,
| CD |
| PA |
而PB与平面PAE所成的角和PB与平面ABCD所成的角相等,
所以:|cos<
| CD |
| PB |
| PA |
| PB |
| ||||
|
|
| ||||
|
|
由第一问知
| CD |
| PA |
| PB |
故|
| -16+0+0 | ||||
2
|
| 0+0+h2 | ||
h•
|
解得h=
8
| ||
| 5 |
又梯形ABCD的面积为S=
| 1 |
| 2 |
所以四棱锥P-ABCD的体积为V=
| 1 |
| 3 |
| 1 |
| 3 |
8
| ||
| 5 |
128
| ||
| 15 |


练习册系列答案
相关题目


 与
与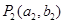 是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组
是直线y=kx+1(k为常数)上两个不同的点,则关于x和y的方程组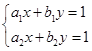 的解的情况是( )
的解的情况是( )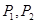 如何,总是无解
如何,总是无解