题目内容
如图,四棱锥P-ABCD的底面是正方形,PA⊥底面ABCD,PA=2,∠PDA=45,点E、F分别为棱AB、PD的中点.

(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.

(1)求证:AF∥平面PCE;
(2)求三棱锥C-BEP的体积.
(1)详见解析;(2)三棱锥 的体积为
的体积为 .
.
 的体积为
的体积为 .
.试题分析:(1)求证:
 ∥平面
∥平面 ,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题欲证
,证明线面平行,首先证明线线平行,可用三角形的中位线平行,也可用平行四边形的对边平行,本题欲证 ∥平面
∥平面 ,根据直线与平面平行的判定定理可知只需证
,根据直线与平面平行的判定定理可知只需证 与平面
与平面 内一直线平行,取
内一直线平行,取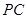 的中点
的中点 ,连接
,连接 ,易证
,易证 ,从而得
,从而得 ∥平面
∥平面 ;(2)求三棱锥
;(2)求三棱锥 的体积,三棱锥
的体积,三棱锥 的体积可转化成三棱锥
的体积可转化成三棱锥 的体积,而
的体积,而 底面
底面 ,从而
,从而 即为三棱锥
即为三棱锥 的高,根据三棱锥的体积公式进行求解即可.
的高,根据三棱锥的体积公式进行求解即可.试题解析:(1)证明:取PC的中点G,连接GF,因为F为PD的中点,
所以,GF∥CD且
 又E为AB的中点,ABCD是正方形,
又E为AB的中点,ABCD是正方形,所以,AE∥CD且
 故AE∥GF且
故AE∥GF且
所以,AEGF是平行四边形,故AF∥EG,而
 平面
平面 ,
, 平面
平面 ,所以,AF∥平面
,所以,AF∥平面 .
.(2)因为PA⊥底面ABCD,所以,PA是三棱锥P-EBC的高,PA⊥AD,PA=2,
∠PDA=450,所以,AD=2,正方形ABCD中,E为AB的中点,所以,EB=1,故
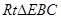 的面积为1,故
的面积为1,故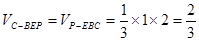 .
.故三棱锥C-BEP的体积为
 .
.
练习册系列答案
相关题目
 的圆锥
的圆锥 中,已知
中,已知 的直径
的直径 ,
, 是
是 的中点,
的中点, 是弦
是弦 的中点.
的中点.
 的平面角,并求出它的大小;
的平面角,并求出它的大小; 与
与 所成的角的正切值.
所成的角的正切值.


 ,8
,8
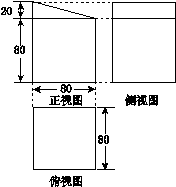
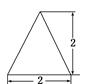
 )cm2
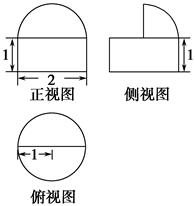
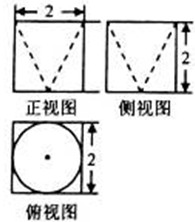
)cm2 的三视图如图,则四棱锥
的三视图如图,则四棱锥