题目内容
【题目】已知函数f(x)=x2﹣|x2﹣ax﹣2|,a为实数.
(1)当a=1时,求函数f(x)在[0,3]上的最小值和最大值;
(2)若函数f(x)在(﹣∞,﹣1)和(2,+∞)上单调递增,求实数a的取值范围.
【答案】
(1)解:当a=1时, ![]()
结合图象可知f(x)在 ![]() 上单调递减,在
上单调递减,在 ![]() 上单调递增,,
上单调递增,,
f(x)在[0,3]上的最小值为 ![]() ,
,
f(x)在[0,3]上的最大值为f(3)=5.
(2)解:令x2﹣ax﹣2=0,∵△=a2+8>0,
必有两根 ![]() ,
, ![]()
∴ ![]()
若函数f(x)在(﹣∞,﹣1)和(2,+∞)上单调递增,
则 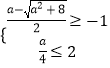 ,解得:1≤a≤8
,解得:1≤a≤8
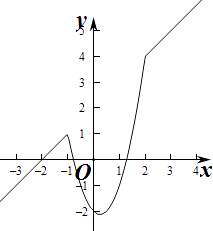
【解析】(1)当a=1时,求出函数f(x)的表达式,结合图象即可求出函数在[0,3]上的最小值和最大值;(2)将函数表示为分段函数形式,结合一元二次函数单调性的性质和关系建立不等式进行求解即可.
【考点精析】本题主要考查了函数的最值及其几何意义的相关知识点,需要掌握利用二次函数的性质(配方法)求函数的最大(小)值;利用图象求函数的最大(小)值;利用函数单调性的判断函数的最大(小)值才能正确解答此题.

练习册系列答案
 直通贵州名校周测月考直通名校系列答案
直通贵州名校周测月考直通名校系列答案
相关题目