题目内容
【题目】如图,游客从某旅游景区的景点A处下山至C处有两种路径.一种是从A沿直线步行到C,另一种是先从A沿索道乘缆车到B,然后从B沿直线步行到C.
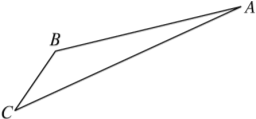
现有甲、乙两位游客从A处下山,甲沿AC匀速步行,速度为50 m/min,在甲出发2 min后,乙从A乘缆车到B,在B处停留1 min后,再从B匀速步行到C.假设缆车匀速直线运行的速度为130 m/min,山路AC长为1 260 m,经测量,cos A=![]() ,cos C=
,cos C=![]() .
.
(1)求索道AB的长;
(2)问乙出发多少分钟后,乙在缆车上与甲的距离最短?
(3)为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在什么范围内?
【答案】(1)1 040 m;(2)![]() ;(3)
;(3)![]() .
.
【解析】(1)在![]() 中,因为cos A=
中,因为cos A=![]() ,cos C=
,cos C=![]() ,所以sin A=
,所以sin A=![]() ,sin C=
,sin C=![]() .
.
从而sin B=sin[π-(A+C)]=sin(A+C)=sin Acos C+cos Asin C=![]() .
.
由正弦定理![]() ,可得
,可得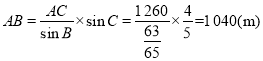 .
.
所以索道AB的长为1 040 m.(3分)
(2)假设乙出发t 分钟后,甲、乙两游客距离为d,此时,甲行走了(100+50t)m,乙距离A处130t m,
所以由余弦定理,得![]() ,
,
因为![]() ,即0≤t≤8,所以当
,即0≤t≤8,所以当![]() 分钟时,甲、乙两游客距离最短.(6分)
分钟时,甲、乙两游客距离最短.(6分)
(3)由正弦定理![]() ,得
,得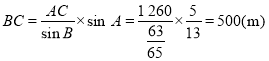 .
.
乙从B出发时,甲已走了50×(2+8+1)=550(m),还需走710 m才能到达C.
设乙步行的速度为v m/min,由题意得![]() ,解得
,解得![]() ,
,
所以为使两位游客在C处互相等待的时间不超过3分钟,乙步行的速度应控制在![]() (单位:m/min)范围内.(10分)
(单位:m/min)范围内.(10分)

【题目】某省数学学业水平考试成绩分为A、B、C、D四个等级,在学业水平成绩公布后,从该省某地区考生中随机抽取60名考生,统计他们的数学成绩,部分数据如下:
等级 | A | B | C | D |
频数 | 24 | 12 | ||
频率 | 0.1 |
(1)补充完成上述表格中的数据;
(2)现按上述四个等级,用分层抽样的方法从这60名考生中抽取10名,在这10名考生中,从成绩A等和B等的所有考生中随机抽取2名,求至少有一名成绩为A等的概率.