题目内容
已知命题p:方程2x2+ax-a2=0在[-1,1]上有解;命题q:只有一个实数x0满足不等式x02+2ax0+2a≤0,若命题“p∨q”是假命题,求实数a的取值范围.
(-∞,-2)∪(2,+∞)
解:由2x2+ax-a2=0得(2x-a)(x+a)=0,
∴x= 或x=-a,
或x=-a,
∴当命题p为真命题时| |≤1或|-a|≤1,∴|a|≤2.
|≤1或|-a|≤1,∴|a|≤2.
又“只有一个实数x0满足x02+2ax0+2a≤0”,
即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴Δ=4a2-8a=0,∴a=0或a=2.
∴当命题q为真命题时,a=0或a=2.
∵命题“p∨q”为假命题,∴p假q假,∴|a|>2,∴a>2或a<-2.
即a的取值范围为(-∞,-2)∪(2,+∞).
∴x=
 或x=-a,
或x=-a,∴当命题p为真命题时|
 |≤1或|-a|≤1,∴|a|≤2.
|≤1或|-a|≤1,∴|a|≤2.又“只有一个实数x0满足x02+2ax0+2a≤0”,
即抛物线y=x2+2ax+2a与x轴只有一个交点,
∴Δ=4a2-8a=0,∴a=0或a=2.
∴当命题q为真命题时,a=0或a=2.
∵命题“p∨q”为假命题,∴p假q假,∴|a|>2,∴a>2或a<-2.
即a的取值范围为(-∞,-2)∪(2,+∞).

练习册系列答案
 暑假作业暑假快乐练西安出版社系列答案
暑假作业暑假快乐练西安出版社系列答案
相关题目
 ,设命题
,设命题 :函数
:函数 在R上单调递增;命题
在R上单调递增;命题 :不等式
:不等式 对任意
对任意 恒成立,若
恒成立,若 的取值范围.
的取值范围.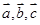 是非零向量,已知命题P:若
是非零向量,已知命题P:若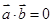 ,
,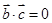 ,则
,则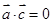 ;命题q:若
;命题q:若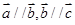 ,则
,则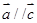 ,则下列命题中真命题是( )
,则下列命题中真命题是( )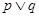
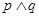
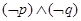
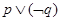
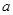 ,则事件“
,则事件“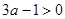 ”发生的概率为
”发生的概率为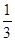 ;
;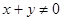 ”是“
”是“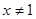 或
或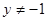 ”的充分不必要条件;
”的充分不必要条件; 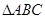 中,若
中,若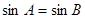 ,则
,则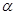 不垂直于平面
不垂直于平面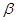 ,那么平面
,那么平面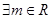 ,使
,使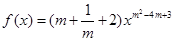 是幂函数;
是幂函数; 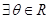 ,使
,使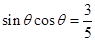 成立;
成立;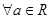 ,使
,使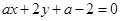 恒过定点;
恒过定点; ,不等式
,不等式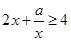 成立的充要条件
成立的充要条件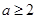 .
.