题目内容
设命题p:函数f(x)=lg(ax2-4x+a)的定义域为R;命题q:不等式2x2+x>2+ax,在x∈(-∞,-1)上恒成立,如果命题“p∨q”为真命题,命题“p∧q”为假命题,求实数a的取值范围.
[1,2]
解:p:Δ<0且a>0,故a>2;
q:a>2x-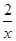 +1对?x∈(-∞,-1)恒成立,
+1对?x∈(-∞,-1)恒成立,
设g(x)=2x-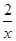 +1,
+1,
则g(x)在(-∞,-1)上单调递增,g(x)<1,故a≥1.
“p∨q”为真命题,命题“p∧q”为假命题,等价于p,q一真一假.
故1≤a≤2,则实数a的取值范围为[1,2].
q:a>2x-
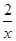 +1对?x∈(-∞,-1)恒成立,
+1对?x∈(-∞,-1)恒成立,设g(x)=2x-
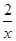 +1,
+1,则g(x)在(-∞,-1)上单调递增,g(x)<1,故a≥1.
“p∨q”为真命题,命题“p∧q”为假命题,等价于p,q一真一假.
故1≤a≤2,则实数a的取值范围为[1,2].

练习册系列答案
相关题目
 ”是“
”是“ 在
在 上为增函数”的充要条件[]
上为增函数”的充要条件[]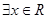 使得
使得 ”的否定是:“
”的否定是:“ ”
” ”是“
”是“ ”的必要不充分条件
”的必要不充分条件 ”,则
”,则 p是真命题
p是真命题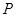 :函数
:函数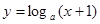 在
在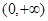 内单调递减;
内单调递减;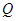 :曲线
:曲线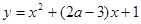 与
与 轴没有交点.如果“
轴没有交点.如果“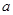 的取值范围是( )
的取值范围是( )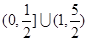
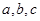 中恰有一个偶数”正确的反设为( )
中恰有一个偶数”正确的反设为( )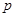 :$
:$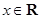 ,
,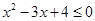 ,则下列说法正确的是( )
,则下列说法正确的是( )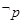 :$
:$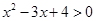 ,且
,且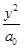 =1为双曲线;命题q:x2-7x+12<0的解集是{x|3<x<4}.给出下列结论:
=1为双曲线;命题q:x2-7x+12<0的解集是{x|3<x<4}.给出下列结论: q”是假命题;
q”是假命题;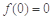 ”是“函数
”是“函数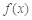 是奇函数”的充要条件
是奇函数”的充要条件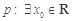 ,
,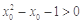 ,则
,则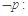
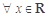 ,
,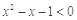
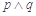 为假命题,则
为假命题,则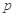 、
、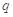 均为假命题
均为假命题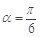 ,则
,则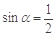 ”的否命题是“若
”的否命题是“若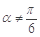 ,则
,则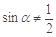 ”
” ,则
,则 或
或 的逆否命题是 .
的逆否命题是 .