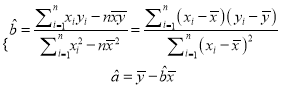题目内容
【题目】（选修4—5：不等式选讲）
已知函数
．
（1）若不等式
的解集为
，求
的值；
（2）若对
，
，求实数
的取值范围．
【答案】（1）
（2）
【解析】
试题分析：（1）根据绝对值定义，将不等式转化为三个不等式组，根据不等式
的解集得形式，只需讨论两种：当
，即
，得
，当
，即
，因此
解得（2）根据绝对值定义，将不等式转化为三个不等式组，当
时，
；当
，
；当
，
；再根据三种情况下不等式恒成立关系，转化对应函数最值
；
；
，最后求它们的交集得
试题解析：（1）
，
法一：由已知得
，．．．．．．．．．．．．．．．．．．．．．．．2分
当，即，得；．．．．．．．．．．．．．．．．．．．．．3分
当，即，．．．．．．．．．．．．．．．．．．．．．．．．．4分
由已知
的解集为
或，则显然．．．．．．．．．．．．．．．．．5分
法二：由已知易得
的图象关于直线
对称，．．．．．．．．．．．．．．3分
又
的解集为
，则
，即
．．．．．．．．5分
（2）法一：不等式
恒成立，即
恒成立．．．．．．．．．．．．．．．．6分
当时，即恒成立，得，解得
；．．．．．．．．．．．．．．．．．．． 7分
当，即恒成立，得，解得
；．．．．．．．．．．．．8分
当，即恒成立，得，解得
．．．．．．．．．．．． 9分
综上得．．．．．．．．．．．．．．．．．10分
法二：不等式
恒成立，即
恒成立，
由图象可知
在
处取得最小值
，．．．．．．．．．．．．．．8分
而
在
处取得最大值，故
，得．．．．．．．．．．．．．．10分
【题目】下表提供了某厂节能降耗技术改造后生产甲产品过程记录的产量
（吨）与相应的生产能耗
（吨标准煤）的几组对照数据：
| 3 | 4 | 5 | 6 |
| 2.5 | 3 | 4 | 4.5 |
（1）已知产量
和能耗
呈线性关系，请根据上表提供的数据，用最小二乘法求出
关于
的线性回归方程
；
（2）已知该厂技改前100吨甲产品的生产耗能为90吨标准煤，试根据（1）求出的线性回归方程，预测生产100吨甲产品的生产能耗比技改前降低多少吨标准煤？
参考公式： 
