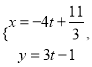题目内容
【题目】已知
分别为
三个内角
的对边，且
．
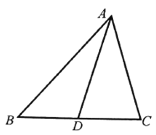
（1）求
；
（2）若
为
边上的中线，
，求的面积．
【答案】（1）
（2）
【解析】
试题分析：（1）先由正弦定理将边化为角：
，再根据三角形内角关系消B角：
，利用两角和正弦公式展开化简得
，再利用配角公式得
，解得（2）利用向量平行四边形法则得
，两边平方，根据向量数量积得
；由同角关系得
，再由正弦定理可得
， 解方程组可得
，代入面积公式可得
试题解析：（1）∵
，由正弦定理得：
，即
，．．．．．．．．．．．．．．．．．．．．．．．．．3分
化简得：，∴．．．．．．．．．．．．．．．．．．5分
在
中，
，∴
，得．．．．．．．．．．．．．．．．．．．．．6分
（2）在
中，
，得．．．．．．．．．．．．．．．．．．．7分
则
．．．．．．．．．．．．．．．．．．．．．．．．8分
由正弦定理得
．．．．．．．．．．．．．．．．．．．．．．．．．．．．9分
设
，在
中，由余弦定理得：
，则
，解得
，
即
．．．．．．．．．．．．．．．．．．．．．．．．．11分
故．．．．．．．．．．．．．．．．．．．．．．．．12分
练习册系列答案
相关题目
【题目】经统计，某医院一个结算窗口每天排队结算的人数及相应的概率如下：
排除人数 | 0--5 | 6--10 | 11--15 | 16--20 | 21--25 | 25人以上 |
概率 | 0.1 | 0.15 | 0.25 | 0.25 | 0.2 | 0.05 |
（1）求每天超过20人排队结算的概率；
（2）求2天中，恰有1天出现超过20人排队结算的概率.
