题目内容
【题目】已知函数![]() ,
,![]() 为自然对数的底数.
为自然对数的底数.
(Ⅰ)讨论![]() 的单调性;
的单调性;
(Ⅱ)若函数![]() 的图象与直线
的图象与直线![]() 交于
交于![]() 两点,线段
两点,线段![]() 中点的横坐标为
中点的横坐标为![]() ,证明:
,证明:![]() (
(![]() 为函数
为函数![]() 的导函数)
的导函数)
【答案】(Ⅰ)详见解析; (Ⅱ)详见解析
【解析】
试题解析:(Ⅰ)由题可知,![]() 然后再,分
然后再,分![]() ,
,![]() ,
,![]() 三种情况,进行讨论,由此即可求出结果.(Ⅱ)化简可得
三种情况,进行讨论,由此即可求出结果.(Ⅱ)化简可得![]() ,可得
,可得![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在![]() 上单调递增,与
上单调递增,与![]() 轴不可能有两个交点,故
轴不可能有两个交点,故![]() .当
.当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .故
.故![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.不妨设
上单调递减.不妨设![]() ,且
,且![]() ,要证
,要证![]() ,需证
,需证![]() ,即证
,即证![]() ,又
,又![]() ,所以只需证
,所以只需证![]() .即证:当
.即证:当![]() 时,
时, ![]() .然后再构造辅助函数,再利用导数,即可证明结果.
.然后再构造辅助函数,再利用导数,即可证明结果.
试题解析:解:(1)由题可知,![]()
①当![]() 时,令
时,令![]() ,则
,则![]() ∴
∴![]()
令![]() ,则
,则![]() ∴
∴![]()
②当![]() 时,
时,![]()
③当![]() 时,令
时,令![]() ,则
,则![]() ∴
∴![]()
令![]() ,则
,则![]() ∴
∴![]()
综上:①当![]() 时,
时,![]() 在
在![]() 上单调递减,在
上单调递减,在![]() 上单调递增.当②
上单调递增.当②
![]() 时,
时,![]() 在
在![]() 上单调递增.
上单调递增.
③当![]() 时,
时,![]() 在
在![]() 上单调递增,在
上单调递增,在![]() 上单调递减.
上单调递减.
(2)∵![]()
∴![]() ,当
,当![]() 时,
时,![]() ,
,![]() 在
在
![]() 上单调递增,与
上单调递增,与![]() 轴不可能有两个交点,故
轴不可能有两个交点,故![]() .
.
当![]() 时,令
时,令![]() ,则
,则![]() ;令
;令![]() ,则
,则![]() .故
.故![]() 在
在![]() 上
上
单调递增,在![]() 上单调递减.不妨设
上单调递减.不妨设![]() ,且
,且![]() ,要证
,要证
![]() ,
,
需证![]() ,即证
,即证![]() ,
,
又![]() ,所以只需证
,所以只需证![]() .即证:当
.即证:当![]() 时,
时,
![]() .
.
设![]()
则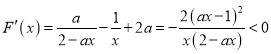 ,∴
,∴![]() 在
在![]() 上
上
单调递减,又![]() ,故
,故![]() .
.

练习册系列答案
相关题目