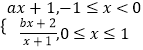题目内容
【题目】某校倡导为特困学生募捐,要求在自动购水机处每购买一瓶矿泉水,便自觉向捐款箱中至少投入一元钱.现统计了连续5天的售出矿泉水箱数和收入情况,列表如下:
售出水量 | 7 | 6 | 6 | 5 | 6 |
收入 | 165 | 142 | 148 | 125 | 150 |
学校计划将捐款以奖学金的形式奖励给品学兼优的特困生,规定:特困生综合考核前20名,获一等奖学金500元;综合考核21-50名,获二等奖学金300元;综合考核50名以后的不获得奖学金.
(1)若![]() 与
与![]() 成线性相关,则某天售出9箱水时,预计收入为多少元?
成线性相关,则某天售出9箱水时,预计收入为多少元?
(2)甲乙两名学生获一等奖学金的概率均为![]() ,获二等奖学金的概率均为
,获二等奖学金的概率均为![]() ,不获得奖学金的概率均为
,不获得奖学金的概率均为![]() ,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和
,已知甲乙两名学生获得哪个等级的奖学金相互独立,求甲乙两名学生所获得奖学金之和![]() 的分布列及数学期望;
的分布列及数学期望;
附:回归方程![]() ,其中
,其中 .
.
【答案】(1)206;(2)![]() .
.
【解析】试题分析:(1)先求出君子,代入公式求![]() ,
,![]() ,再求线性回归方程自变量为9的函数值,(2)先确定随机变量取法,在利用概率乘法求对应概率,列表可得分布列,根据数学期望公式求期望.
,再求线性回归方程自变量为9的函数值,(2)先确定随机变量取法,在利用概率乘法求对应概率,列表可得分布列,根据数学期望公式求期望.
试题解析:
(1)![]() ,经计算
,经计算![]() ,所以线性回归方程为
,所以线性回归方程为![]() ,
,
当![]() 时,
时,![]() 的估计值为206元;
的估计值为206元;
(2)![]() 的可能取值为0,300,500,600,800,1000;
的可能取值为0,300,500,600,800,1000;
![]() ;
;![]() ;
;![]() ;
;
![]() ;
;![]() ;
;![]() ;
;
| 0 | 300 | 500 | 600 | 800 | 1000 |
|
|
|
|
|
|
|
所以![]() 的数学期望
的数学期望![]() .
.

 活力课时同步练习册系列答案
活力课时同步练习册系列答案 学业测评一课一测系列答案
学业测评一课一测系列答案【题目】某种机器零件转速在符合要求的范围内使用时间随机器运转速度的变化而变化,某检测员随机收集了20个机器零件的使用时间与转速的数据,列表如下:
机器转速(转/分) | 189 | 193 | 190 | 185 | 183 | 202 | 187 | 203 | 192 | 201 |
零件使用时间(月) | 43 | 33 | 39 | 37 | 38 | 37 | 38 | 35 | 38 | 35 |
机器转速(转/分) | 193 | 197 | 191 | 186 | 191 | 188 | 185 | 204 | 201 | 189 |
零件使用时间(月) | 37 | 40 | 41 | 37 | 35 | 37 | 42 | 36 | 34 | 40 |
(Ⅰ)若“转速大于200转/分”为“高速”,“转速不大于200转/分”为“非高速”,“使用时间大于36个月”的为“长寿命”,“使用时间不大于36个月”的为“非长寿命”,请根据上表数据完成下面的![]() 列联表:
列联表:
高速 | 非高速 | 合计 | |
长寿命 | |||
非长寿命 | |||
合计 |
(Ⅱ)根据(Ⅰ)中的![]() 列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
列联表,试运用独立性检验的思想方法:能否在犯错误的概率不超过0.01的前提下认为零件使用寿命的长短与转速高低之间的关系.
参考公式:![]() ,其中
,其中![]() .
.
参考数据:
| 0.050 | 0.010 | 0.005 | 0.001 |
3.841 | 6.635 | 7.879 | 10.828 |