Question

【题目】已知f（x）=aln（x﹣1），g（x）=x2+bx，F（x）=f（x+1）﹣g（x），其中a，b∈R．
（1）若y=f（x）与y=g（x）的图象在交点（2，k）处的切线互相垂直，求a，b的值；
（2）若x=2是函数F（x）的一个极值点，x0和1是F（x）的两个零点，且x0∈（n，n+1）n∈N，求n．

Answer 1

【答案】
（1）解：f′（x）= ，g′（x）=2x+b，

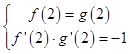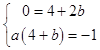由题知 ，即 ，解得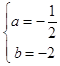

（2）解：F（x）=f（x+1）﹣g（x）=alnx﹣x2﹣bx，F ．

由题知 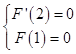，即 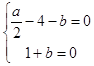，解得a=6，b=﹣1，

∴F（x）=6lnx﹣x2+x，F = ，

∵x＞0，由F′（x）＞0，解得0＜x＜2；由F′（x）＜0，解得x＞2，

∴F（x）在（0，2）上单调递增，在（2，+∞）单调递减，

故F（x）至多有两个零点，其中x1∈（0，2），x2∈（2，+∞），

又F（2）＞F（1）=0，F（3）=6（ln3﹣1）＞0，F（4）=6（ln4﹣2）＜0，

∴x0∈（3，4），故n=3

【解析】（1）根据导数的几何意义建立切线斜率之间的关系建立方程，求a，b的值；（2）根据导数和函数极值之间的关系建立方程，即可求n；
【考点精析】通过灵活运用函数的极值与导数，掌握求函数的极值的方法是:（1）如果在附近的左侧,右侧,那么是极大值（2）如果在附近的左侧,右侧,那么是极小值即可以解答此题．