题目内容
【题目】已知椭圆![]() :
:![]() 的离心率为
的离心率为![]() ,椭圆
,椭圆![]() :
:![]() 经过点
经过点![]() .
.
(1)求椭圆![]() 的标准方程;
的标准方程;
(2)设点![]() 是椭圆
是椭圆![]() 上的任意一点,射线
上的任意一点,射线![]() 与椭圆
与椭圆![]() 交于点
交于点![]() ,过点
,过点![]() 的直线
的直线![]() 与椭圆
与椭圆![]() 有且只有一个公共点,直线
有且只有一个公共点,直线![]() 与椭圆
与椭圆![]() 交于
交于![]() ,
,![]() 两个相异点,证明:
两个相异点,证明:![]() 面积为定值.
面积为定值.
【答案】(1)![]() ; (2)见解析.
; (2)见解析.
【解析】
(1)根据椭圆的离心率和把过的点代入椭圆方程,根据得到的式子求出![]() .
.
(2)当直线![]() 斜率不存在时,易得
斜率不存在时,易得![]() 的面积,当直线
的面积,当直线![]() 斜率存在时,设为
斜率存在时,设为![]() ,与椭圆
,与椭圆![]() 相切,得到
相切,得到![]() 和
和![]() 的关系,再由直线
的关系,再由直线![]() 和椭圆联立方程组,得到
和椭圆联立方程组,得到![]() 、
、![]() ,
,
利用弦长公式表示出![]() ,再得到
,再得到![]() 和
和![]() 的关系,由
的关系,由![]() 到
到![]() 的距离,得到
的距离,得到![]() 到
到![]() 的距离,从而计算出
的距离,从而计算出![]() 的面积.得到结论为定值.
的面积.得到结论为定值.
(1)解:因为![]() 的离心率为
的离心率为![]() ,
,
所以![]() ,
,
解得![]() .①
.①
将点![]() 代入
代入![]() ,整理得
,整理得![]() .②
.②
联立①②,得![]() ,
,![]() ,
,
故椭圆![]() 的标准方程为
的标准方程为![]() .
.
(2)证明:①当直线![]() 的斜率不存在时,
的斜率不存在时,
点![]() 为
为![]() 或
或![]() ,由对称性不妨取
,由对称性不妨取![]() ,
,
由(1)知椭圆![]() 的方程为
的方程为![]() ,所以有
,所以有![]() .
.
将![]() 代入椭圆
代入椭圆![]() 的方程得
的方程得![]() ,
,
所以![]()
![]() .
.
②当直线![]() 的斜率存在时,设其方程为
的斜率存在时,设其方程为![]() ,
,
将![]() 代入椭圆
代入椭圆![]() 的方程
的方程
得![]() ,
,
由题意得![]() ,
,
整理得![]() .
.
将![]() 代入椭圆
代入椭圆![]() 的方程,
的方程,
得![]() .
.
设![]() ,
,![]() ,
,
则![]() ,
,![]() ,
,
所以![]()
![]() .
.
设![]() ,
,![]() ,
,![]() ,则可得
,则可得![]() ,
,![]() .
.
因为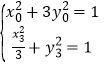 ,所以
,所以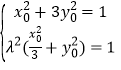 ,
,
解得![]() (
(![]() 舍去),
舍去),
所以![]() ,从而
,从而![]() .
.
又因为点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以点![]() 到直线
到直线![]() 的距离为
的距离为![]() ,
,
所以![]()
![]() ,
,
综上,![]() 的面积为定值
的面积为定值![]() .
.

练习册系列答案
相关题目
【题目】某高校在2017年的自主招生考试成绩中随机抽取100名学生的笔试成绩,按成绩分组,得到的频率分布表如表:
组号 | 分组 | 频率 |
第1组 |
|
|
第2组 |
|
|
第3组 |
|
|
第4组 |
|
|
第5组 |
|
|

![]() 求出频率分布表中
求出频率分布表中![]() 处应填写的数据,并完成如图所示的频率分布直方图;
处应填写的数据,并完成如图所示的频率分布直方图;
![]() 根据直方图估计这次自主招生考试笔试成绩的平均数和中位数
根据直方图估计这次自主招生考试笔试成绩的平均数和中位数![]() 结果都保留两位小数
结果都保留两位小数![]() .
.