题目内容
【题目】在平面直角坐标系中，以坐标原点为中心，以坐标轴为对称轴的帮圆C经过点M（2，1），N
.
（1）求椭圆C的标准方程；
（2）经过点M作倾斜角互补的两条直线，分别与椭圆C相交于异于M点的A，B两点，当△AMB面积取得最大值时，求直线AB的方程.
【答案】（1）
（2）
或
【解析】
（1）设椭圆C的方程为
（
，
，
）.
根据椭圆过
两点，代入得到方程组，解得.
（2）由直线AM，BM，AB的斜率存在，故.设它们的斜率分别为
，
，k.
设
，
，直线AB的方程为
.联立直线与椭圆方程，消元列出韦达定理，由
.即
. 即可解得
，或
.分别代入检验，再用弦长公式及点到直线的距离公式，表示出三角形的面积，利用基本不等式求最值.
解：（1）设椭圆C的方程为（，，）.
∵点
和N
在椭圆C上，
∴
.解得
.
∴椭圆C的标准方程为
.
（2）∵点A，B为椭圆上异于M的两点，且直线AM，BM的倾斜角互补，
∴直线AM，BM，AB的斜率存在.设它们的斜率分别为，，k.
设，，直线AB的方程为.
∴.
∴.
由
，消去y，得
.
由
，得
.
∴
，
.
∴
.
∴
.
∴
.
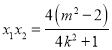∴，或.
∵点A，B为椭圆上异于M的两点，
∴当时，直线AB的方程为
，不合题意，舍去.
∴直线AB的斜率为
.
∵
，点M到直线AB的距离为
，
∴
的面积为
.
当且仅当
时，
的面积取得最大值，此时
.
∵，满足.
∴直线AB的方程为或.
练习册系列答案
相关题目
【题目】已知从甲地到乙地的公路里程约为240（单位：km）.某汽车每小时耗油量Q（单位：L）与速度x（单位：
）（
）的关系近似符合以下两种函数模型中的一种（假定速度大小恒定）：①
，②
，经多次检验得到以下一组数据：
x | 0 | 40 | 60 | 120 |
Q | 0 |
|
| 20 |
（1）你认为哪一个是符合实际的函数模型，请说明理由；
（2）从甲地到乙地，这辆车应以多少速度行驶才能使总耗油量最少？
