题目内容
17.已知点A(-1,3),B(5,7),直线l:3x+4y-20=0(1)过点A且与直线l平行的直线方程;
(2)过点B且与直线l垂直的直线方程.
分析 (1)根据两直线平行,斜率相等,求出直线的斜率,用点斜式求得直线l1的方程.
(2)根据两直线垂直,斜率之积等于-1,求出直线的斜率,用点斜式求得直线的方程.
解答 解:(1)3x+4y-20=0的斜率为$-\frac{3}{4}$,因为两条直线平行,所以过点A且与直线l平行的直线斜率为$-\frac{3}{4}$,
代入点斜式,得y-3=-$\frac{3}{4}$(x+1),
化简,得3x+4y-9=0.
(2)过点B且与直线l垂直的直线斜率为$\frac{4}{3}$,由点斜式得到y-7=$\frac{4}{3}$(x-5),整理得4x-3y+1=0.
点评 本题考查用点斜式求直线方程的方法,两直线平行、垂直的性质,求出直线的斜率是解题的关..

练习册系列答案
相关题目
7.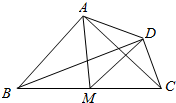 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
 如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )
如图,四边形ABCD满足$\overrightarrow{AB}$•$\overrightarrow{AC}$=$\overrightarrow{DB}$•$\overrightarrow{DC}$=0,|$\overrightarrow{AB}$|=2|$\overrightarrow{DC}$|=2,若M是BC的中点,则$\overrightarrow{AB}$•$\overrightarrow{AM}$-$\overrightarrow{DM}$•$\overrightarrow{DC}$=( )| A. | 1 | B. | -1 | C. | -$\frac{3}{2}$ | D. | $\frac{3}{2}$ |
6.函数y=cos2x-sin2x的图象可以由函数y=cos2x+sin2x的图象经过下列哪种变换得到( )
| A. | 向右平移$\frac{3π}{4}$ | B. | 向右平移π | C. | 向左平移$\frac{π}{2}$ | D. | 向左平移π |
7.下列说法正确的是( )
| A. | 若一个平面内的两条直线与另一个平面都平行,那么这两个平面相互平行 | |
| B. | 若一个平面经过另一个平面的垂线,那么这两个平面相互垂直 | |
| C. | 垂直于同一直线的两条直线相互平行 | |
| D. | 若两个平面都垂直于第三个平面,则这两个平面平行 |