题目内容
.如图，在长方体ABCD-A1B1C1D1中，AB=BC=2,AA1=1,则BC1与平面BB1D1D所成角的余弦值为
A． | B． | C． | D． |
C
分析：连接A1C1交B1D1于点O，连接BO，在长方体中由AB=BC=2，可得CO1⊥B1D1，由长方体的性质可证有OC1⊥BB1，且
由直线与平面垂直的判定定理可得OC1⊥平面BB1D1D，则∠C1BO为则BC1与平面BB1D1D所成角
在Rt△BOC1中，可求
解：连接A1C1交B1D1于点O，连接BO
由AB=BC=2，可得A1B1C1D1为正方形即CO1⊥B1D1
由长方体的性质可知BB1⊥面A1B1C1D1，从而有OC1⊥BB1，且BB1∩B1D1=B1
∴OC1⊥平面BB1D1D
则∠C1BO为则BC1与平面BB1D1D所成角
在Rt△BOC1中，OC1=
，BC1=
OB=
∴cos∠OBC1=
=
=故选C．
练习册系列答案
科学实验活动册系列答案
相关题目
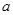的菱形，侧面PAD为正三角形，其所在的平面垂直于底面ABCD．若G为AD的中点，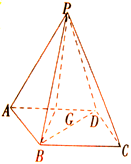
中，
的中点，则异面直线
与
所成角的余弦值为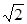 
BB1，则AB1与C1B所成的角的大小为（ ）
中，
为顶点在底面上的射影，且
，则直线
与平面
所成角的大小等于 
，点M,N分别为棱SC、SA的中点，则异面直线AM与BN所成角的余弦值为_______.
的二面角
内，
于
，
于
，且
，则
的长为 。