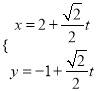题目内容
【题目】设![]() ,正项数列
,正项数列![]() 的前
的前![]() 项的积为
项的积为![]() ,且
,且![]() ,当
,当![]() 时,
时, ![]() 都成立.
都成立.
(1)若![]() ,
, ![]() ,
, ![]() ,求数列
,求数列![]() 的前
的前![]() 项和;
项和;
(2)若![]() ,
, ![]() ,求数列
,求数列![]() 的通项公式.
的通项公式.
【答案】(1) ![]() (2)
(2) ![]()
【解析】试题分析:(1)直接利用递推关系式求出数列的通项公式.
(2)根据已知条件和数列的等量关系求出数列的通项公式.
试题解析:
(1)当n≥2时,因为M={1},所以![]() =TnT1,可得an+1=ana1,
=TnT1,可得an+1=ana1,
故![]() =a1=3(n≥2).
=a1=3(n≥2).
又a1=![]() ,a2=3
,a2=3![]() ,则{an}是公比为3的等比数列,
,则{an}是公比为3的等比数列,
故{an}的前n项和为![]() =
=![]() 3n﹣
3n﹣![]() .
.
(2)当n>k时,因为![]() =TnTk,所以
=TnTk,所以![]() =Tn+1Tk,
=Tn+1Tk,
所以![]() =
=![]() ,即
,即![]() =an+1,
=an+1,
因为M={3,4},所以取k=3,当n>3时,有an+4an﹣2=an+12;
取k=4,当n>4时,有an+5an﹣3=an+12.
由an+5an﹣3=an+12 知,
数列a2,a6,a10,a14,a18,a22,…,a4n﹣2,…,是等比数列,设公比为q.…①
由an+4an﹣2=an+1 知,
数列a2,a5,a8,a11,a14,a17,…,a3n﹣1,…,是等比数列,设公比为q1,…②
数列a3,a6,a9,a12,a15,a18,…,a3n,…,成等比数列,设公比为q2,…③
数列a4,a7,a10,a13,a16,a19,a22,…,a3n+1,…,成等比数列,设公比为q3,…④
由①②得, ![]() =q3,且
=q3,且![]() =q14,所以q1=
=q14,所以q1=![]() ;
;
由①③得, ![]() =q3,且
=q3,且![]() =q24,所以q2=
=q24,所以q2=![]() ;
;
由①④得, ![]() =q3,且
=q3,且![]() =q34,所以q3=
=q34,所以q3=![]() ;
;
所以q1=q2=q3=![]() .
.
由①③得,a6=a2q,a6=a3q2,所以![]() =
=![]() =
=![]() ,
,
由①④得,a10=a2q2,a10=a4q32,所以![]() =
=![]() ,
,
所以a2,a3,a4是公比为q![]() 的等比数列,所以{an}(n≥2)是公比为q
的等比数列,所以{an}(n≥2)是公比为q![]() 的等比数列.
的等比数列.
因为当n=4,k=3时,T7T1=T42T32;
当n=5,k=4时,T9T1=T52T42,
所以(![]() )7=2a24,且(
)7=2a24,且(![]() )10=2a26,所以
)10=2a26,所以![]() =2,a2=2
=2,a2=2![]() .
.
又a1=![]() ,所以{an}(n∈N*)是公比为
,所以{an}(n∈N*)是公比为![]() 的等比数列.
的等比数列.
故数列{an}的通项公式是an=2n﹣1![]() .
.

【题目】2016年1月1日,我国全面实行二孩政策,某机构进行了街头调查,在所有参与调查的青年男女中,持“响应”“犹豫”和“不响应”态度的人数如下表所示:
响应 | 犹豫 | 不响应 | |
男性青年 | 500 | 300 | 200 |
女性青年 | 300 | 200 | 300 |
根据已知条件完成下面的![]() 列联表,并判断能否有
列联表,并判断能否有![]() 的把握认为犹豫与否与性别有关?请说明理由.
的把握认为犹豫与否与性别有关?请说明理由.
犹豫 | 不犹豫 | 总计 | |
男性青年 | |||
女性青年 | |||
总计 | 1800 |
参考公式:![]()
参考数据:
| 0.150 | 0.100 | 0.050 | 0.025 | 0.010 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 |