题目内容
(12分)
如图,正方形ABCD-A1B1C1D1中,E、F、G分别是AB,AD,AA1的中点,

(1)求证AC1⊥平面EFG,
(2)求异面直线EF与CC1所成的角。
如图,正方形ABCD-A1B1C1D1中,E、F、G分别是AB,AD,AA1的中点,

(1)求证AC1⊥平面EFG,
(2)求异面直线EF与CC1所成的角。
解:(1) ∵C1B1⊥面A1ABB1, A1B⊥AB1 由三垂线定理得AC1⊥A1B

∵EF//AB, AC1⊥EF, 同理可证AC1⊥GF
∵GF与EF是平面EFG内的两条相交直线,∴AC1⊥面EFG
(2) ∵E,F分别是AA1,AB的中点,∴EF//A1B
∵B1B//C1C ∴∠A1BB1就是异面直线EF与C1C所成的角
在RT⊿A1BB1中,∠ABB=45º
∴EF与CC所成的角为45º

∵EF//AB, AC1⊥EF, 同理可证AC1⊥GF
∵GF与EF是平面EFG内的两条相交直线,∴AC1⊥面EFG
(2) ∵E,F分别是AA1,AB的中点,∴EF//A1B
∵B1B//C1C ∴∠A1BB1就是异面直线EF与C1C所成的角
在RT⊿A1BB1中,∠ABB=45º
∴EF与CC所成的角为45º
略

练习册系列答案
 应用题天天练四川大学出版社系列答案
应用题天天练四川大学出版社系列答案
相关题目
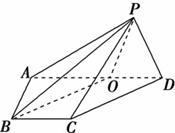
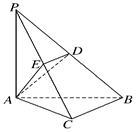 (2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;
(2)当D为PB的中点时,求AD与平面PAC所成的角的正弦值;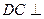 平面ABC,EB//DC,AC=BC=EB=2DC=2,
平面ABC,EB//DC,AC=BC=EB=2DC=2,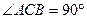 ,P、Q分别为DE、AB的中点。
,P、Q分别为DE、AB的中点。
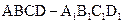 中,E是棱
中,E是棱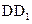 的中点.
的中点.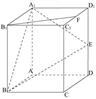
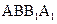 所成的角的正弦值;
所成的角的正弦值;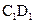 上是否存在一点F,使
上是否存在一点F,使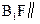 平面
平面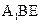 ?证明你的结论.
?证明你的结论. 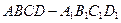 中,
中,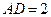 ,
,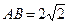 ,
,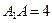 ,
,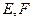 分别是
分别是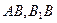 的中点.
的中点.
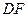 ⊥平面
⊥平面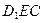 ;
;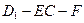 的大小.
的大小.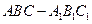 中,
中,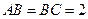 ,
,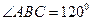 ,又顶点
,又顶点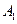 在底面
在底面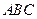 上的射影落在
上的射影落在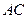 上,侧棱
上,侧棱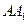 与底面
与底面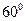 角,
角,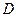 为
为
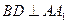 ;
;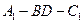 为直二面角,试求侧棱
为直二面角,试求侧棱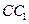 与侧面
与侧面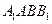 的距离.
的距离.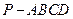 的底面
的底面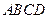 是一个边长为4的正方形,侧面
是一个边长为4的正方形,侧面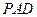 是正三角形,侧面
是正三角形,侧面 底面
底面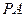 与平面
与平面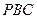 所成的角的正弦值。
所成的角的正弦值。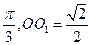 ,则
,则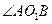 =( )
=( )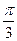 B.
B.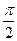 C.
C.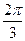 D.
D.