题目内容
(本小题满分12分)
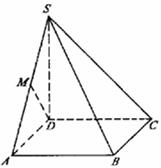
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.
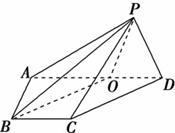
(1)若CD∥平面PBO,试指出点O的位置,并说明理由;
(2)求证:平面PAB⊥平面PCD.
如图,在四棱锥P-ABCD中,侧面PAD⊥底面ABCD,侧棱PA⊥PD,底面ABCD是直角梯形,其中BC∥AD,∠BAD=90°,AD=3BC,O是AD上一点.

(1)若CD∥平面PBO,试指出点O的位置,并说明理由;
(2)求证:平面PAB⊥平面PCD.
解:(1)答: O在AD的 处且离D点比较近. ┅┅┅┅┅┅┅2分
理由是:
∵CD∥平面PBO,
CD?平面ABCD,且平面ABCD∩平面PBO=BO,
∴BO∥CD, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅3分
又∵BC∥AD,
∴四边形BCDO为平行四边形,┅┅┅┅┅┅┅┅┅┅┅4分
∴BC=DO,
又∵AD=3BC,
∴点O的位置满足=,
即在AD的处且离D点比较近.┅┅┅┅┅┅┅┅┅┅6分
(2)证明:
∵侧面PAD⊥底面ABCD,
AB?底面ABCD,且AB⊥交线AD,
∴AB⊥平面PAD, ┅┅┅┅┅┅┅┅┅┅┅┅8分
∵PD 平面PAD
平面PAD
∴AB⊥PD. ┅┅┅┅┅┅┅┅┅┅┅┅9分
又∵PA⊥PD,
PA?平面PAB,AB?平面PAB,
AB∩PA=A, ┅┅┅┅┅┅┅┅┅┅10分
∴PD⊥平面PAB. ┅┅┅┅┅┅┅┅┅┅11分
又∵PD?平面PCD,
∴平面PAB⊥平面PCD. ┅┅┅┅┅┅┅┅┅┅12分
理由是:
∵CD∥平面PBO,
CD?平面ABCD,且平面ABCD∩平面PBO=BO,
∴BO∥CD, ┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅┅3分
又∵BC∥AD,
∴四边形BCDO为平行四边形,┅┅┅┅┅┅┅┅┅┅┅4分
∴BC=DO,
又∵AD=3BC,
∴点O的位置满足=,
即在AD的处且离D点比较近.┅┅┅┅┅┅┅┅┅┅6分
(2)证明:
∵侧面PAD⊥底面ABCD,
AB?底面ABCD,且AB⊥交线AD,
∴AB⊥平面PAD, ┅┅┅┅┅┅┅┅┅┅┅┅8分
∵PD
 平面PAD
平面PAD∴AB⊥PD. ┅┅┅┅┅┅┅┅┅┅┅┅9分
又∵PA⊥PD,
PA?平面PAB,AB?平面PAB,
AB∩PA=A, ┅┅┅┅┅┅┅┅┅┅10分
∴PD⊥平面PAB. ┅┅┅┅┅┅┅┅┅┅11分
又∵PD?平面PCD,
∴平面PAB⊥平面PCD. ┅┅┅┅┅┅┅┅┅┅12分

略

练习册系列答案
相关题目
 的高
的高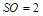 ,底边长
,底边长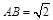 ,则异面直线
,则异面直线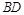 和
和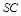 之间的距离( )
之间的距离( )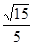
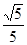
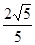
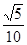
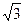 .
.
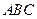 的边长为4,
的边长为4,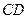 是
是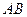 边上的高,
边上的高,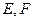 分别是
分别是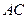 和
和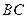 边的中点,现将△
边的中点,现将△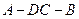 .
.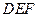 的位置关系,并
的位置关系,并 说明理由;
说明理由;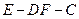 的余弦值;
的余弦值;
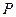 ,使
,使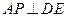 ?证明你的结论.
?证明你的结论. 

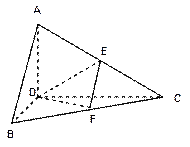
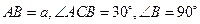 , D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角
, D为AC的中点,E为BD的中点,AE的延长线交BC于F,将△ABD沿BD折起,二面角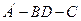 的大小记为
的大小记为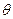 .
.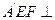 平面BCD;
平面BCD; 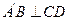 时,求
时,求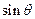 的值;
的值;  的距离.
的距离.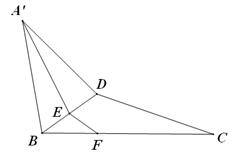

 中
中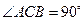 ,
, 平面
平面 ,此图形中有 个直角三角形.
,此图形中有 个直角三角形.