题目内容
12.已知关于x的一次函数y=ax+b,(1)设集合P={-2,-1,1,2,3}和Q={-2,0,3},分别从集合P和Q中随机取一个数作为a和b,求函数y=ax+b是增函数的概率;
(2)实数a,b满足条件$\left\{{\begin{array}{l}{-1≤a≤1}\\{-1≤b≤1}\\{a+b-1≤0}\end{array}}\right.$求函数y=ax+b的图象经过二、三、四象限的概率.
分析 (1)是古典概型,只要求出所有事件个数以及满足条件的事件个数,利用古典概型公式解答;
(2)是几何概型,分别求出已知区域的面积以及满足条件的区域面积,利用面积比求概率.
解答 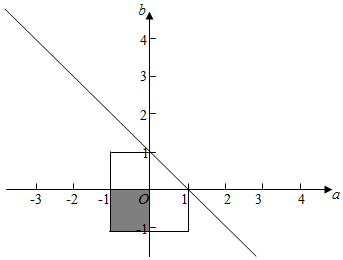 解:(1)由已知a≠0,集合P={-2,-1,1,2,3}和Q={-2,0,3},分别从集合P和Q中随机取一个数作为a和b,
解:(1)由已知a≠0,集合P={-2,-1,1,2,3}和Q={-2,0,3},分别从集合P和Q中随机取一个数作为a和b,
所有事件有5×3=15个,设A事件为:函数y=ax+b是增函数的3×3=9个,由古典概型的概率公式得到,$P(A)=\frac{9}{15}=\frac{3}{5}$;
(2)线性约束条件$\left\{{\begin{array}{l}{-1≤a≤1}\\{-1≤b≤1}\\{a+b-1≤0}\end{array}}\right.$所表示的区域面积S=$\frac{7}{2}$,
要使函数y=ax+b的图象经过二、三、四象限,则实数a,b必须满足条件$\left\{{\begin{array}{l}{-1≤a<0}\\{-1≤b≤0}\\{a+b-1≤0}\end{array}}\right.$,如图阴影部分,
其面积为S1=1,所求的概率为P=$\frac{S_1}{S}$=$\frac{2}{7}$.
点评 本题考查了古典概型和几何概型的概率求法;关键是明确概率模型,利用公式解答.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目
2.某同学为了解秋冬季节用电量(y度)与气温(x℃)的关系,由下表数据计算出回归直线方程为y=-2x+60,则表中a的值为( )
| 气温 | 18 | 13 | 10 | -1 |
| 用电量(度) | 24 | 34 | a | 64 |
| A. | 40 | B. | 39 | C. | 38 | D. | 37 |