题目内容
19.设F(c,0)为双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的右焦点,点B的坐标为(0,b).若圆(x-c)2+y2=r2(r>0)与双曲线的渐近线相切,且|FB|≥$\sqrt{3}$r,则该双曲线的离心率e的取值范围是( )| A. | $(1,\sqrt{2}]$ | B. | $[\sqrt{2},+∞)$ | C. | $(1,\sqrt{3}]$ | D. | $[\sqrt{3},+∞)$ |
分析 利用圆(x-c)2+y2=r2(r>0)与双曲线的渐近线相切,可得r=b,利用|FB|≥$\sqrt{3}$r,即可求出双曲线的离心率e的取值范围.
解答 解:双曲线$\frac{x^2}{a^2}-\frac{y^2}{b^2}$=1(a>0,b>0)的一条渐近线方程为bx-ay=0,
因为圆(x-c)2+y2=r2(r>0)与双曲线的渐近线相切,
所以$\frac{|bc|}{\sqrt{{b}^{2}+{a}^{2}}}$=r,所以r=b,
因为|FB|≥$\sqrt{3}$r,
所以$\sqrt{{b}^{2}+{c}^{2}}$≥$\sqrt{3}$b,
所以$\frac{1}{2}$c2≥b2,
所以$\frac{1}{2}$c2≥c2-a2,
因为e>1,所以1<e≤$\sqrt{2}$.
故选:A.
点评 熟练掌握圆的标准方程、双曲线的渐近线方程、圆与直线相切的性质、点到直线的距离公式是解题的关键.

练习册系列答案
相关题目
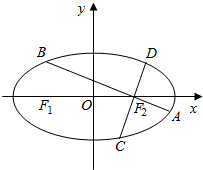 如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.
如图,已知椭圆$\frac{x^2}{a^2}$+$\frac{y^2}{b^2}$=1(a>b>0)的离心率为$\frac{1}{2}$,过椭圆右焦点F2作两条互相垂直的弦AB与CD,当直线AB的斜率为0时,|AB|+|CD|=7.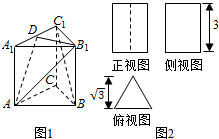 已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.
已知某几何体的直观图(图1)与它的三视图(图2),其中俯视图为正三角形,其它两个视图是矩形,已知D是棱A1C1的中点.