题目内容
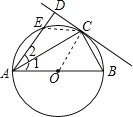
【题目】如图,AB为⊙O的直径,点E在⊙O上,C为 ![]() 的中点,过点C作直线CD⊥AE于D,连接AC、BC.
的中点,过点C作直线CD⊥AE于D,连接AC、BC.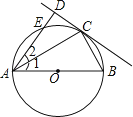
(1)试判断直线CD与⊙O的位置关系,并说明理由;
(2)若AD=2,AC= ![]() ,求AB的长.
,求AB的长.
【答案】
(1)
解:相切,连接OC,
∵C为 ![]() 的中点,
的中点,
∴∠1=∠2,
∵OA=OC,
∴∠1=∠ACO,
∴∠2=∠ACO,
∴AD∥OC,
∵CD⊥AD,
∴OC⊥CD,
∴直线CD与⊙O相切;
(2)
解:方法1:连接CE,
∵AD=2,AC= ![]() ,
,
∵∠ADC=90°,
∴CD= ![]() =
= ![]() ,
,
∵CD是⊙O的切线,
∴CD2=ADDE,
∴DE=1,
∴CE= ![]() =
= ![]() ,
,
∵C为 ![]() 的中点,
的中点,
∴BC=CE= ![]() ,
,
∵AB为⊙O的直径,
∴∠ACB=90°,
∴AB= ![]() =3.
=3.
方法2:∵∠DCA=∠B,
易得△ADC∽△ACB,
∴ ![]() =
= ![]() ,
,
∴AB=3.
【解析】本题考查了直线与圆的位置关系,切线的判定和性质,圆周角定理,勾股定理,平行线的性质,切割线定理,熟练掌握各定理是解题的关键.(1)连接OC,由C为 ![]() 的中点,得到∠1=∠2,等量代换得到∠2=∠ACO,根据平行线的性质得到OC⊥CD,即可得到结论;
的中点,得到∠1=∠2,等量代换得到∠2=∠ACO,根据平行线的性质得到OC⊥CD,即可得到结论;
(2)连接CE,由勾股定理得到CD= ![]() =
= ![]() ,根据切割线定理得到CD2=ADDE,根据勾股定理得到CE=
,根据切割线定理得到CD2=ADDE,根据勾股定理得到CE= ![]() =
= ![]() ,由圆周角定理得到∠ACB=90°,即可得到结论.
,由圆周角定理得到∠ACB=90°,即可得到结论.
【考点精析】通过灵活运用直线与圆的三种位置关系,掌握直线与圆有三种位置关系:无公共点为相离;有两个公共点为相交,这条直线叫做圆的割线;圆与直线有唯一公共点为相切,这条直线叫做圆的切线,这个唯一的公共点叫做切点即可以解答此题.

【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.