题目内容
【题目】图1是某公交公司1路车从起点站A站途经B站和C站,最终到达终点站D站的格点站路线图.(8×8的格点图是由边长为1的小正方形组成)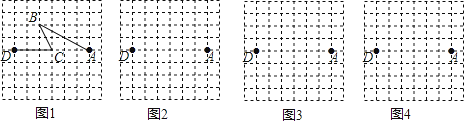
(1)求1路车从A站到D站所走的路程(精确到0.1);
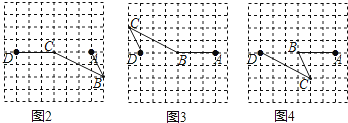
(2)在图2、图3和图4的网格中各画出一种从A站到D站的路线图.(要求:①与图1路线不同、路程相同;②途中必须经过两个格点站;③所画路线图不重复)
【答案】
(1)
解:根据图1可得: ![]() ,
, ![]() ,CD=3
,CD=3
∴A站到B站的路程= AB+BC+CD=2 ![]() +
+ ![]() +3=3+3
+3=3+3 ![]() ≈9.7;
≈9.7;
(2)
解:从A站到D站的路线图如下:
【解析】本题主要考查了作图,解决问题的关键是掌握勾股定理以及图形的基本变换.在作图时要理解题意,弄清问题中对所作图形的要求,结合对应几何图形的性质和基本作图的方法作图.
(1)先根据网格求得AB、BC、CD三条线段的长,再相加求得所走的路程的近似值;
(2)根据轴对称、平移或中心对称等图形的变换进行作图即可.

练习册系列答案
相关题目
【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为 .