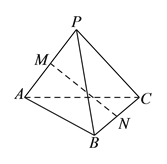
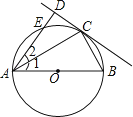
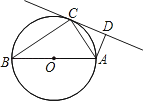
题目内容
【题目】在生产过程中,测得纤维产品的纤度(表示纤维粗细的一种量)共有100个数据,将数据分组如表:
分组 | 频数 |
|
|
|
|
|
|
|
|
|
|
|
|
合计 |
|
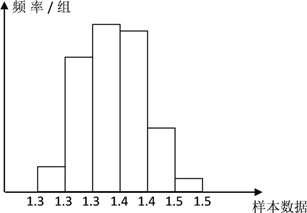
(1)画出频率分布表,并画出频率分布直方图;
(2)估计纤度落在![]() 中的概率及纤度小于
中的概率及纤度小于![]() 的概率是多少?
的概率是多少?
(3)从频率分布直方图估计出纤度的众数、中位数和平均数.
【答案】(1)详见解析;(2)0.69,0.44;(3)1.40,1.408.
【解析】试题分析:(1)根据表中数据,即可画出频率分布表及频率分布直方图;
(2)根据频率分布直方图,可以得出相应频率,从而得到落在相应区间内的概率;
(3)根据直方图,及众数、中位数的概念可求出,并计算平均数.
试题解析:(1)频率分布表,频率分布直方图如下图:
分组 | 频数 | 频率 |
| 4 | 0.04 |
| 25 | 0.25 |
| 30 | 0.30 |
| 29 | 0.29 |
| 10 | 0.10 |
| 2 | 0.02 |
合计 | 100 | 1.00 |
(2)纤度落在![]() 中的概率约为
中的概率约为![]() ,
,
纤度小于1.40的概率约为![]() .
.
(3)总体数据的众数:1.40,中位数:1.408,平均数:1.4088.

【题目】为了解少年儿童的肥胖是否与常喝碳酸饮料有关,现对30名六年级学生进行了问卷调查得到如下列联表:
常喝 | 不常喝 | 合计 | |
肥胖 | 2 | ||
不肥胖 | 18 | ||
合计 | 30 |
已知在全部30人中随机抽取1人,抽到肥胖的学生的概率为![]() .
.
(1)请将上面的列表补充完整;
(2)是否有99.5%的把握认为肥胖与常喝碳酸饮料有关?说明你的理由;
(3)4名调查人员随机分成两组,每组2人,一组负责问卷调查,另一组负责数据处理,求工作人员甲分到负责收集数据组,工作人员乙分到负责数据处理组的概率.
参考数据:
| 0.15 | 0.10 | 0.05 | 0.025 | 0.010 | 0.005 | 0.001 |
| 2.072 | 2.706 | 3.841 | 5.024 | 6.635 | 7.879 | 10.828 |
(参考公式: 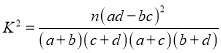 )
)
【题目】中央电视台为了解该卫视《朗读者》节目的收视情况,抽查东西两部各![]() 个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
个城市,得到观看该节目的人数(单位:千人)如下茎叶图所示其中一个数字被污损,
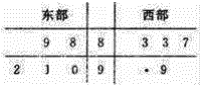
(1)求东部各城市观看该节目观众平均人数超过西部各城市观看该节目观众平均人数的概率.
(2)随着节目的播出,极大激发了观众对朗读以及经典的阅读学习积累的热情,从中获益匪浅,现从观看节目的观众中随机统计了![]() 位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
位观众的周均阅读学习经典知识的时间(单位:小时)与年龄(单位:岁),并制作了对照表(如下表所示):
年龄 |
|
|
|
|
周均学习成语知识时间 |
|
|
|
|
由表中数据,试求线性回归方程![]() ,并预测年龄为
,并预测年龄为![]() 岁观众周均学习阅读经典知识的时间.
岁观众周均学习阅读经典知识的时间.
【题目】林业部门要考察某种幼树在一定条件下的移植成活率,下表是这种幼树在移植过程中的一组数据:
移植的棵数n | 1000 | 1500 | 2500 | 4000 | 8000 | 15000 | 20000 | 30000 |
成活的棵数m | 865 | 1356 | 2220 | 3500 | 7056 | 13170 | 17580 | 26430 |
成活的频率 | 0.865 | 0.904 | 0.888 | 0.875 | 0.882 | 0.878 | 0.879 | 0.881 |
估计该种幼树在此条件下移植成活的概率为 .